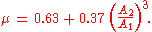Borda–Carnot equation
Encyclopedia
In fluid dynamics
the Borda–Carnot equation is an empirical
description of the mechanical energy losses of the fluid
due to a (sudden) flow expansion. It describes how the total head reduces due to the losses. This in contrast with Bernoulli's principle
for dissipation
less flow (without irreversible losses), where the total head is a constant along a streamline. The equation is named after Jean-Charles de Borda
(1733–1799) and Lazare Carnot
(1753–1823).
This equation is used both for open channel flow
as well as in pipe flow
s. In parts of the flow where the irreversible energy losses are negligible, Bernoulli's principle can be used.
where
In case of an abrupt and wide expansion the loss coefficient is equal to one. In other instances, the loss coefficient has to be determined by other means, most often from empirical formula
e (based on data obtained by experiment
s). The Borda–Carnot loss equation is only valid for decreasing velocity, v1 > v2, otherwise the loss ΔE is zero — without mechanical work
by additional external force
s there cannot be a gain in mechanical energy of the fluid.
The loss coefficient ξ can be influenced by streamlining. For example in case of a pipe expansion, the use of a gradual expanding diffuser
can reduce the mechanical energy losses.
. For an incompressible flow the result is — for two locations labelled 1 and 2, with location 2 downstream to 1 — along a streamline:
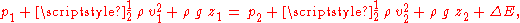
with
The first three terms, on either side of the equal sign are respectively the pressure, the kinetic energy
density of the fluid and the potential energy
density due to gravity. As can be seen, pressure acts effectively as a form of potential energy.
In case of high-pressure pipe flows, when gravitational effects can be neglected, ΔE is equal to the loss Δ(p+½ρv2):
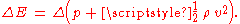
For open channel flow
s, ΔE is related to the total head loss ΔH as:
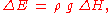with H the total head: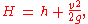 
where h is the hydraulic head
— the free surface
elevation above a reference datum: h = z + p/(ρg).
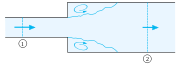The Borda–Carnot equation is applied to the flow through a sudden expansion of a horizontal pipe. At cross section 1, the mean flow velocity is equal to v1, the pressure is p1 and the cross-sectional area is A1. The corresponding flow quantities at cross section 2 — after the expansion — are v2, p2 and A2, respectively. The loss coefficient ξ for this sudden expansion is equal to one: ξ = 1.0. Due to mass conservation, assuming a constant fluid density
ρ, the volumetric flow rate
through both cross sections 1 and 2 has to be equal:
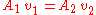so 
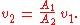
Consequently — according to the Borda–Carnot equation — the mechanical energy loss in this sudden expansion is:
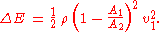
The corresponding loss of total head ΔH is:
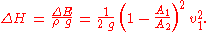
For this case with ξ = 1, the total change in kinetic energy between the two cross sections is dissipated. As a result, the pressure change between both cross sections is (for this horizontal pipe without gravity effects):
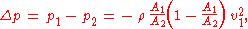
and the change in hydraulic head h = z + p/(ρg):
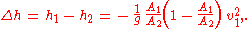
The minus signs, in front of the right-hand sides, mean that the pressure (and hydraulic head) are larger after the pipe expansion.
That this change in the pressures (and hydraulic heads), just before and after the pipe expansion, corresponds with an energy loss becomes clear when comparing with the results of Bernoulli's principle
. According to this dissipationless principle, a reduction in flow speed is associated with a much larger increase in pressure than found in the present case with mechanical energy losses.
In case of a sudden reduction of pipe diameter, without streamlining, the flow is not be able to follow the sharp bend into the narrower pipe. As a result, there is flow separation
, creating recirculating separation zones at the entrance of the narrower pipe. The main flow is contracted between the separated flow areas, and later on expands again to cover the full pipe area.
There is not much head loss between cross section 1, before the contraction, and cross section 3, the vena contracta
at which the main flow is contracted most. But there are substantial losses in the flow expansion from cross section 3 to 2. These head losses can be expressed by using the Borda–Carnot equation, through the use of the coefficient of contraction μ:
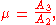
with A3 the cross-sectional area at the location of strongest main flow contraction 3, and A2 the cross-sectional area of the narrower part of the pipe. Since A3 ≤ A2, the coefficient of contraction is less than one: μ ≤ 1. Again there is conservation of mass, so the volume fluxes in the three cross sections are a constant (for constant fluid density ρ):
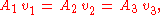
with v1, v2 and v3 the mean flow velocity in the associated cross sections. Then, according to the Borda–Carnot equation (with loss coefficient ξ=1), the energy loss ΔE per unit of fluid volume and due to the pipe contraction is:
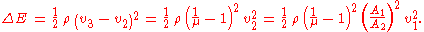
The corresponding loss of total head ΔH can be computed as ΔH = ΔE/(ρg).
According to measurements by Weisbach
, the contraction coefficient for a sharp-edged contraction is approximately:
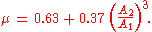
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
the Borda–Carnot equation is an empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
description of the mechanical energy losses of the fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
due to a (sudden) flow expansion. It describes how the total head reduces due to the losses. This in contrast with Bernoulli's principle
Bernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
for dissipation
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
less flow (without irreversible losses), where the total head is a constant along a streamline. The equation is named after Jean-Charles de Borda
Jean-Charles de Borda
Jean-Charles, chevalier de Borda was a French mathematician, physicist, political scientist, and sailor.-Life history:...
(1733–1799) and Lazare Carnot
Lazare Carnot
Lazare Nicolas Marguerite, Comte Carnot , the Organizer of Victory in the French Revolutionary Wars, was a French politician, engineer, and mathematician.-Education and early life:...
(1753–1823).
This equation is used both for open channel flow
Open channel flow
Open-Channel Flow, a branch of Hydraulics, is a type of liquid flow within a conduit with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways, but differ in one important respect; the free surface...
as well as in pipe flow
Pipe flow
Pipe flow, a branch of Hydraulics and Fluid Mechanics, is a type of liquid flow within a closed conduit . The other type of flow within a conduit being open channel flow....
s. In parts of the flow where the irreversible energy losses are negligible, Bernoulli's principle can be used.
Formulation
The Borda–Carnot equation is:where
- ΔE is the fluid's mechanical energy loss,
- ξ is an empirical loss coefficient, which is dimensionless and has a value between zero and one, 0 ≤ ξ ≤ 1,
- ρ is the fluid densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, - v1 and v2 are the mean flow velocitiesFlow velocityIn fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
before and after the expansion.
In case of an abrupt and wide expansion the loss coefficient is equal to one. In other instances, the loss coefficient has to be determined by other means, most often from empirical formula
Empirical formula
In chemistry, the empirical formula of a chemical compound is the simplest positive integer ratio of atoms of each element present in a compound. An empirical formula makes no reference to isomerism, structure, or absolute number of atoms. The empirical formula is used as standard for most ionic...
e (based on data obtained by experiment
Experiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
s). The Borda–Carnot loss equation is only valid for decreasing velocity, v1 > v2, otherwise the loss ΔE is zero — without mechanical work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
by additional external force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s there cannot be a gain in mechanical energy of the fluid.
The loss coefficient ξ can be influenced by streamlining. For example in case of a pipe expansion, the use of a gradual expanding diffuser
Diffuser
Diffuser can refer to any device that diffuses in some manner such as:* In aerodynamics** Diffuser , a shaped section of a car's underbody which improves the car's aerodynamic properties** divergent part of the flute...
can reduce the mechanical energy losses.
Relation to the total head and Bernoulli's principle
The Borda–Carnot equation gives the decrease in the constant of the Bernoulli equationBernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
. For an incompressible flow the result is — for two locations labelled 1 and 2, with location 2 downstream to 1 — along a streamline:
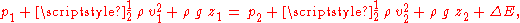
with
- p1 and p2 the pressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
at location 1 and 2, - z1 and z2 the vertical elevation — above some reference level — of the fluid particle, and
- g the gravitational accelerationEarth's gravityThe gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
.
The first three terms, on either side of the equal sign are respectively the pressure, the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
density of the fluid and the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
density due to gravity. As can be seen, pressure acts effectively as a form of potential energy.
In case of high-pressure pipe flows, when gravitational effects can be neglected, ΔE is equal to the loss Δ(p+½ρv2):
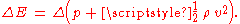
For open channel flow
Open channel flow
Open-Channel Flow, a branch of Hydraulics, is a type of liquid flow within a conduit with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways, but differ in one important respect; the free surface...
s, ΔE is related to the total head loss ΔH as:
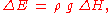with H the total head: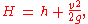 where h is the hydraulic head
Hydraulic head
Hydraulic head or piezometric head is a specific measurement of water pressure above a geodetic datum. It is usually measured as a water surface elevation, expressed in units of length, at the entrance of a piezometer...
— the free surface
Free surface
In physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...
elevation above a reference datum: h = z + p/(ρg).
Sudden expansion of a pipe
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
ρ, the volumetric flow rate
Volumetric flow rate
The volumetric flow rate in fluid dynamics and hydrometry, is the volume of fluid which passes through a given surface per unit time...
through both cross sections 1 and 2 has to be equal:
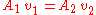so 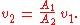Consequently — according to the Borda–Carnot equation — the mechanical energy loss in this sudden expansion is:
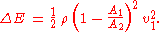
The corresponding loss of total head ΔH is:
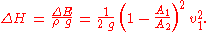
For this case with ξ = 1, the total change in kinetic energy between the two cross sections is dissipated. As a result, the pressure change between both cross sections is (for this horizontal pipe without gravity effects):
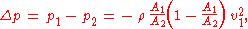
and the change in hydraulic head h = z + p/(ρg):
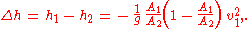
The minus signs, in front of the right-hand sides, mean that the pressure (and hydraulic head) are larger after the pipe expansion.
That this change in the pressures (and hydraulic heads), just before and after the pipe expansion, corresponds with an energy loss becomes clear when comparing with the results of Bernoulli's principle
Bernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
. According to this dissipationless principle, a reduction in flow speed is associated with a much larger increase in pressure than found in the present case with mechanical energy losses.
Sudden contraction of a pipe
Flow separation
All solid objects travelling through a fluid acquire a boundary layer of fluid around them where viscous forces occur in the layer of fluid close to the solid surface. Boundary layers can be either laminar or turbulent...
, creating recirculating separation zones at the entrance of the narrower pipe. The main flow is contracted between the separated flow areas, and later on expands again to cover the full pipe area.
There is not much head loss between cross section 1, before the contraction, and cross section 3, the vena contracta
Vena contracta
Vena contracta is the point in a fluid stream where the diameter of the stream is the least, such as in the case of a stream issuing out of a nozzle,...
at which the main flow is contracted most. But there are substantial losses in the flow expansion from cross section 3 to 2. These head losses can be expressed by using the Borda–Carnot equation, through the use of the coefficient of contraction μ:
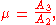
with A3 the cross-sectional area at the location of strongest main flow contraction 3, and A2 the cross-sectional area of the narrower part of the pipe. Since A3 ≤ A2, the coefficient of contraction is less than one: μ ≤ 1. Again there is conservation of mass, so the volume fluxes in the three cross sections are a constant (for constant fluid density ρ):
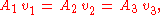
with v1, v2 and v3 the mean flow velocity in the associated cross sections. Then, according to the Borda–Carnot equation (with loss coefficient ξ=1), the energy loss ΔE per unit of fluid volume and due to the pipe contraction is:
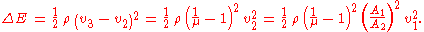
The corresponding loss of total head ΔH can be computed as ΔH = ΔE/(ρg).
According to measurements by Weisbach
Julius Weisbach
Julius Ludwig Weisbach was a German mathematician and engineer.-Life and work:...
, the contraction coefficient for a sharp-edged contraction is approximately: