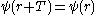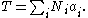Born-von Karman boundary condition
Encyclopedia
The Born–von Karman boundary condition is a set of boundary conditions which impose the restriction that a wave function must be periodic
on a certain Bravais lattice. (Named after Max Born
and Theodore Von Karman
). This condition is often applied in solid state physics to model an ideal crystal
.
The condition can be stated as
where i runs over the dimension
s of the Bravais lattice, the ai are the primitive vectors of the lattice, and the Ni are any integers (assuming the lattice is infinite). This definition can be used to show that
for any lattice translation vector T such that:
Note, however, the Born–von Karman boundary conditions are useful when Ni are large (infinite).
The Born–von Karman boundary condition is important in solid state physics for analyzing many features of crystals, such as diffraction
and the band gap
. Modeling the potential
of a crystal as a periodic function with the Born–von Karman boundary condition and plugging in Schrödinger's equation
results in a proof of Bloch's theorem
, which is particularly important in understanding the band structure of crystals.
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
on a certain Bravais lattice. (Named after Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
and Theodore Von Karman
Theodore von Karman
Theodore von Kármán was a Hungarian-American mathematician, aerospace engineer and physicist who was active primarily in the fields of aeronautics and astronautics. He is responsible for many key advances in aerodynamics, notably his work on supersonic and hypersonic airflow characterization...
). This condition is often applied in solid state physics to model an ideal crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
.
The condition can be stated as
where i runs over the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s of the Bravais lattice, the ai are the primitive vectors of the lattice, and the Ni are any integers (assuming the lattice is infinite). This definition can be used to show that
for any lattice translation vector T such that:
Note, however, the Born–von Karman boundary conditions are useful when Ni are large (infinite).
The Born–von Karman boundary condition is important in solid state physics for analyzing many features of crystals, such as diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
and the band gap
Electronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
. Modeling the potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
of a crystal as a periodic function with the Born–von Karman boundary condition and plugging in Schrödinger's equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
results in a proof of Bloch's theorem
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
, which is particularly important in understanding the band structure of crystals.