Borsuk's conjecture
Encyclopedia
The Borsuk problem in geometry, for historical reasons incorrectly called a Borsuk conjecture
, is a question in discrete geometry
.
showed that an ordinary 3-dimensional ball
in Euclidean space
can be easily dissected into 4 solids, each of which has a smaller diameter
than the ball, and generally d-dimensional ball can be covered with compact
sets of diameters smaller than the ball. At the same time he proved that d subset
s are not enough in general. The proof is based on the Borsuk–Ulam theorem
. That led Borsuk to a general question:
Translation:
The question got a positive answer in the following cases:
The problem was finally solved in 1993 by Jeff Kahn and Gil Kalai
, who showed the general answer to the Borsuk's question is no. Their construction shows that pieces do not suffice for and for each .
The current best bound, due to Aicke Hinrichs and Christian Richter, shows that the answer is negative for all .
Apart from finding the minimum number d of dimensions such that the number of pieces
mathematicians are interested in finding the general behavior of 
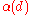function. Kahn and Kalai show that in general (that is for d big enough), one needs 
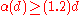number of pieces. They also quote the upper bound by Oded Schramm
, who showed that for every ε, if d is sufficiently large,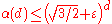
. The correct order of magnitude of α(d) is still unknown (see e.g. Alon's article), however it is conjectured that there is a constant such that 
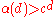for all .
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
, is a question in discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
.
Problem
In 1932 Karol BorsukKarol Borsuk
Karol Borsuk was a Polish mathematician.His main interest was topology.Borsuk introduced the theory of absolute retracts and absolute neighborhood retracts , and the cohomotopy groups, later called Borsuk-Spanier cohomotopy groups. He also founded the so called Shape theory...
showed that an ordinary 3-dimensional ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
can be easily dissected into 4 solids, each of which has a smaller diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
than the ball, and generally d-dimensional ball can be covered with compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
sets of diameters smaller than the ball. At the same time he proved that d subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s are not enough in general. The proof is based on the Borsuk–Ulam theorem
Borsuk–Ulam theorem
In mathematics, the Borsuk–Ulam theorem, named after Stanisław Ulam and Karol Borsuk, states that every continuous function from an n-sphere into Euclidean n-space maps some pair of antipodal points to the same point....
. That led Borsuk to a general question:
- Die folgende Frage bleibt offen: Lässt sich jede beschränkte Teilmenge E des Raumes
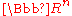in (n + 1) Mengen zerlegen, von denen jede einen kleineren Durchmesser als E hat?
Translation:
- The following question remains open: Can every boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
subset E of the space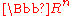
be partitionedPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
into (n + 1) sets, each of which has a smaller diameter than E?
The question got a positive answer in the following cases:
- d = 2 — the original result by Borsuk (1932).
- d = 3 — the result of H. G. Eggleston (1955). A simple proof was found later by Branko GrünbaumBranko GrünbaumBranko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
and Aladár Heppes. - For all d for the smooth convex bodies — the result of Hugo HadwigerHugo HadwigerHugo Hadwiger was a Swiss mathematician, known for his work in geometry, combinatorics, and cryptography.-Biography:...
(1946). - For all d for centrally-symmetricRotational symmetryGenerally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
bodies (A.S. Riesling, 1971). - For all d for bodies of revolutionSolid of revolutionIn mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....
— the result of Boris Dekster (1995).
The problem was finally solved in 1993 by Jeff Kahn and Gil Kalai
Gil Kalai
Gil Kalai is the Henry and Manya Noskwith Professor of Mathematics at the Hebrew University of Jerusalem, and adjunct professor of mathematics and of computer science at Yale University, and the editor of the Israel Journal of Mathematics.-Biography:...
, who showed the general answer to the Borsuk's question is no. Their construction shows that pieces do not suffice for and for each .
The current best bound, due to Aicke Hinrichs and Christian Richter, shows that the answer is negative for all .
Apart from finding the minimum number d of dimensions such that the number of pieces
mathematicians are interested in finding the general behavior of 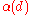function. Kahn and Kalai show that in general (that is for d big enough), one needs 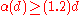number of pieces. They also quote the upper bound by Oded SchrammOded Schramm
Oded Schramm was an Israeli-American mathematician known for the invention of the Schramm–Loewner evolution and for working at the intersection of conformal field theory and probability theory.-Biography:...
, who showed that for every ε, if d is sufficiently large,
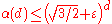. The correct order of magnitude of α(d) is still unknown (see e.g. Alon's article), however it is conjectured that there is a constant such that 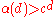for all .See also
- Hadwiger's conjectureHadwiger conjecture (combinatorial geometry)In combinatorial geometry, the Hadwiger conjecture states that any convex body in n-dimensional Euclidean space can be covered by 2n or fewer smaller bodies homothetic with the original body, and that furthermore, the upper bound of 2n is necessary iff the body is a parallelpiped...
on covering convex bodies with smaller copies of themselves
Further reading
- Oleg Pikhurko, Algebraic Methods in Combinatorics, course notes.