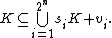Hadwiger conjecture (combinatorial geometry)
Encyclopedia
In combinatorial geometry, the Hadwiger conjecture states that any convex body
in n-dimensional Euclidean space
can be covered by 2n or fewer smaller bodies homothetic with the original body, and that furthermore, the upper bound of 2n is necessary iff
the body is a parallelpiped. There also exists an equivalent formulation in terms of the number of floodlights needed to illuminate the body.
The Hadwiger conjecture is named after Hugo Hadwiger
, who included it on a list of unsolved problems in 1957; it was, however, previously studied by and independently, . Additionally, there is a different Hadwiger conjecture
concerning graph coloring
—and in some sources the geometric Hadwiger conjecture is also called the Levi–Hadwiger conjecture or the Hadwiger–Levi covering problem.
The conjecture remains unsolved even in three dimensions, though the two dimensional case was resolved by .
convex set
in the n-dimensional Euclidean space
Rn, then there exists a set of 2n scalar
s si and a set of 2n translation vector
s vi such that all si lie in the range 0 < si < 1, and
Furthermore, the upper bound is necessary iff K is a parallelepiped, in which case all 2n of the scalars may be chosen to be equal to 1/2.
, the problem is equivalent to one of illumination: how many floodlights must be placed outside of an opaque convex body in order to completely illuminate its exterior? For the purposes of this problem, a body is only considered to be illuminated if for each point of the boundary of the body, there is at least one floodlight that is separated from the body by all of the tangent planes intersecting the body on this point; thus, although the faces of a cube may be lit by only two floodlights, the planes tangent to its vertices and edges cause it to need many more lights in order for it to be fully illuminated. For any convex body, the number of floodlights needed to completely illuminate it turns out to equal the number of smaller copies of the body that are needed to cover it.
may be covered by n + 1 copies of itself, scaled by a factor of n/(n + 1). However, covering a square by smaller squares (with parallel sides to the original) requires four smaller squares, as each one can cover only one of the larger square's four corners. In higher dimensions, covering a hypercube
or more generally a parallelepiped
by smaller homothetic copies of the same shape requires a separate copy for each of the vertices
of the original hypercube or parallelepiped; because these shapes have 2n vertices, 2n smaller copies are necessary. This number is also sufficient: a cube or parallelepiped may be covered by 2n copies, scaled by a factor of 1/2. Hadwiger's conjecture is that parallelepipeds are the worst case for this problem, and that any other convex body may be covered by fewer than 2n smaller copies of itself.
In three dimensions it is known that sixteen copies always suffice, but this is still far from the conjectured bound of eight copies.
The conjecture is known to hold for certain special classes of convex bodies, including symmetric polyhedra and bodies of constant width
in three dimensions. The number of copies needed to cover any zonotope is at most (3/4)2n, while for bodies with a smooth surface (that is, having a single tangent plane per boundary point), at most n + 1 smaller copies are needed to cover the body, as Levi
already proved.
Convex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
in n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
can be covered by 2n or fewer smaller bodies homothetic with the original body, and that furthermore, the upper bound of 2n is necessary iff
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the body is a parallelpiped. There also exists an equivalent formulation in terms of the number of floodlights needed to illuminate the body.
The Hadwiger conjecture is named after Hugo Hadwiger
Hugo Hadwiger
Hugo Hadwiger was a Swiss mathematician, known for his work in geometry, combinatorics, and cryptography.-Biography:...
, who included it on a list of unsolved problems in 1957; it was, however, previously studied by and independently, . Additionally, there is a different Hadwiger conjecture
Hadwiger conjecture (graph theory)
In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...
concerning graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
—and in some sources the geometric Hadwiger conjecture is also called the Levi–Hadwiger conjecture or the Hadwiger–Levi covering problem.
The conjecture remains unsolved even in three dimensions, though the two dimensional case was resolved by .
Formal statement
Formally, the Hadwiger conjecture is: If K is any boundedBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
in the n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, then there exists a set of 2n scalar
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
s si and a set of 2n translation vector
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s vi such that all si lie in the range 0 < si < 1, and
Furthermore, the upper bound is necessary iff K is a parallelepiped, in which case all 2n of the scalars may be chosen to be equal to 1/2.
Alternate formulation with illumination
As shown by BoltyanskyVladimir Boltyansky
Vladimir Grigorevich Boltyansky , also transliterated as Boltyanski, Boltyanskii, or Boltjansky, is a Soviet and Russian mathematician, educator and author of popular mathematical books and articles. He is best known for his books on topology, combinatorial geometry and Hilbert's third problem.-...
, the problem is equivalent to one of illumination: how many floodlights must be placed outside of an opaque convex body in order to completely illuminate its exterior? For the purposes of this problem, a body is only considered to be illuminated if for each point of the boundary of the body, there is at least one floodlight that is separated from the body by all of the tangent planes intersecting the body on this point; thus, although the faces of a cube may be lit by only two floodlights, the planes tangent to its vertices and edges cause it to need many more lights in order for it to be fully illuminated. For any convex body, the number of floodlights needed to completely illuminate it turns out to equal the number of smaller copies of the body that are needed to cover it.
Examples
As shown in the illustration, a triangle may be covered by three smaller copies of itself, and more generally in any dimension a simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
may be covered by n + 1 copies of itself, scaled by a factor of n/(n + 1). However, covering a square by smaller squares (with parallel sides to the original) requires four smaller squares, as each one can cover only one of the larger square's four corners. In higher dimensions, covering a hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
or more generally a parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
by smaller homothetic copies of the same shape requires a separate copy for each of the vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of the original hypercube or parallelepiped; because these shapes have 2n vertices, 2n smaller copies are necessary. This number is also sufficient: a cube or parallelepiped may be covered by 2n copies, scaled by a factor of 1/2. Hadwiger's conjecture is that parallelepipeds are the worst case for this problem, and that any other convex body may be covered by fewer than 2n smaller copies of itself.
Known results
The two-dimensional case was settled by : every two-dimensional bounded convex set may be covered with four smaller copies of itself, with the fourth copy needed only in the case of parallelograms. However, the conjecture remains open in higher dimensions except for some special cases. The best known upper bound on the number of smaller copies needed to cover a given body is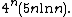
In three dimensions it is known that sixteen copies always suffice, but this is still far from the conjectured bound of eight copies.
The conjecture is known to hold for certain special classes of convex bodies, including symmetric polyhedra and bodies of constant width
Surface of constant width
In geometry, a surface of constant width is a convex form whose width, measured by the distance between two opposite parallelplanes touching its boundary, is the same regardless of the direction of those two parallel planes. One defines the width of the surface in a given direction to be the...
in three dimensions. The number of copies needed to cover any zonotope is at most (3/4)2n, while for bodies with a smooth surface (that is, having a single tangent plane per boundary point), at most n + 1 smaller copies are needed to cover the body, as Levi
Friedrich Wilhelm Levi
Friedrich Wilhelm Daniel Levi was a German mathematician known for his work in abstract algebra. He also worked in geometry, topology, set theory, and analysis...
already proved.