In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Borsuk–Ulam theorem, named after Stanisław Ulam and Karol Borsuk

Karol Borsuk

Karol Borsuk was a Polish mathematician.His main interest was topology.Borsuk introduced the theory of absolute retracts and absolute neighborhood retracts , and the cohomotopy groups, later called Borsuk-Spanier cohomotopy groups. He also founded the so called Shape theory...

, states that every continuous function

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

 from an n-sphere into Euclidean n-space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 maps some pair of antipodal point

Antipodal point

In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....

s to the same point.
Here, two points on a sphere are called antipodal if they are in exactly opposite directions from the sphere's center.

According to , the first historical mention of the statement of this theorem appears in . The first proof was given by , where the formulation of the problem was attributed to Ulam. Since then, many alternate proofs have been found out by various authors as collected in .

The case n = 2 is often illustrated by saying that at any moment there is always a pair of antipodal points on the Earth

Earth

Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...

's surface with equal temperatures and equal barometric pressures. This assumes that temperature and barometric pressure vary continuously.

A stronger statement related to Borsuk–Ulam theorem is that every antipode-preserving map f from Sⁿ to itself has odd degree.

Corollaries

• No subset of Rⁿ is homeomorphic to Sⁿ.
• The Lusternik–Schnirelmann theorem: If the sphere
  Sphere
  A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
  
   Sⁿ is covered by n + 1 open sets, then one of these sets contains a pair (x, −x) of antipodal points. (this is equivalent to the Borsuk–Ulam theorem)
• The Ham sandwich theorem
  Ham sandwich theorem
  In measure theory, a branch of mathematics, the ham sandwich theorem, also called the Stone–Tukey theorem after Arthur H. Stone and John Tukey, states that given measurable "objects" in -dimensional space, it is possible to divide all of them in half with a single -dimensional hyperplane...
  
  : For any compact
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
   sets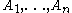 in Rⁿ we can always find a hyperplane dividing each of them into two subsets of equal measure).
• The Brouwer fixed point theorem
  Brouwer fixed point theorem
  Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
  
   .

See also

• Sperner's lemma
  Sperner's lemma
  In mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which follows from it. Sperner's lemma states that every Sperner coloring of a triangulation of an n-dimensional simplex contains a cell colored with a complete set of colors...
  
  
• Tucker's lemma
• Topological combinatorics
  Topological combinatorics
  The discipline of combinatorial topology used combinatorial concepts in topology and in the early 20th century this gradually turned into the field of algebraic topology....
  
  
• Necklace splitting problem
  Necklace splitting problem
  In mathematics, and in particular combinatorics, the necklace splitting problem arises in a variety of contexts including exact division; its picturesque name is due to mathematicians Noga Alon and Douglas B. West....
  
  
• Kakutani's theorem (geometry)
  Kakutani's theorem (geometry)
  Kakutani's theorem is a result in geometry named after Shizuo Kakutani. It states that every convex body in 3-dimensional space has a circumscribed cube, i.e. a cube all whose faces touch the body. The result was further generalized by Yamabe and Yujobô to higher dimension, and by Floyd to other...
  
  
• Isovariant