Boruvka's algorithm
Encyclopedia
Borůvka's algorithm is an algorithm
for finding a minimum spanning tree
in a graph for which all edge weights are distinct.
It was first published in 1926 by Otakar Borůvka
as a method of constructing an efficient electricity network for Moravia
.
The algorithm was rediscovered by Choquet
in 1938; again by Florek, Łukasiewicz, Perkal, Steinhaus
, and Zubrzycki in 1951; and again by Sollin
in 1965. Because Sollin was the only computer scientist in this list living in an English speaking country, this algorithm is frequently called Sollin's algorithm, especially in the parallel computing
literature.
The algorithm begins by first examining each vertex and adding the cheapest edge from that vertex to another in the graph, without regard to already added edges, and continues joining these groupings in a like manner until a tree spanning all vertices is completed.
1 Begin with a connected graph G containing edges of distinct weights, and an empty set of edges T
2 While the vertices of G connected by T are disjoint:
3 Begin with an empty set of edges E
4 For each component:
5 Begin with an empty set of edges S
6 For each vertex in the component:
7 Add the cheapest edge from the vertex in the component to another vertex in a disjoint component to S
8 Add the cheapest edge in S to E
9 Add the resulting set of edges E to T.
10 The resulting set of edges T is the minimum spanning tree of G.
Borůvka's algorithm can be shown to take O
(log V) iterations of the outer loop until it terminates, and therefore to run in time O
(Elog V), where E is the number of edges, and V is the number of vertices in G. In planar graph
s, and more generally in families of graphs closed under graph minor operations, it can be made to run in linear time, by removing all but the cheapest edge between each pair of components after each stage of the algorithm.
Other algorithms for this problem include Prim's algorithm
(actually discovered by Vojtěch Jarník
) and Kruskal's algorithm
. Faster algorithms can be obtained by combining Prim's algorithm with Borůvka's. A faster randomized minimum spanning tree algorithm based in part on Borůvka's algorithm due to Karger, Klein, and Tarjan runs in expected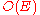
time. The best known (deterministic) minimum spanning tree algorithm by Bernard Chazelle
is also based in part on Borůvka's and runs in O(E α(V)) time, where α is the inverse of the Ackermann function
. These randomized and deterministic algorithms combine steps of Borůvka's algorithm, reducing the number of components that remain to be connected, with steps of a different type that reduce the number of edges between pairs of components.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for finding a minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
in a graph for which all edge weights are distinct.
It was first published in 1926 by Otakar Borůvka
Otakar Boruvka
Otakar Borůvka was a Czech mathematician best known today for his work in graph theory, long before this was an established mathematical discipline....
as a method of constructing an efficient electricity network for Moravia
Moravia
Moravia is a historical region in Central Europe in the east of the Czech Republic, and one of the former Czech lands, together with Bohemia and Silesia. It takes its name from the Morava River which rises in the northwest of the region...
.
The algorithm was rediscovered by Choquet
Gustave Choquet
Gustave Choquet was a French mathematician.Choquet was born in Solesmes, Nord. His contributions include work in functional analysis, potential theory, topology and measure theory...
in 1938; again by Florek, Łukasiewicz, Perkal, Steinhaus
Hugo Steinhaus
Władysław Hugo Dionizy Steinhaus was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the University of Lwów, where he helped establish what later became known as the Lwów School of Mathematics...
, and Zubrzycki in 1951; and again by Sollin
in 1965. Because Sollin was the only computer scientist in this list living in an English speaking country, this algorithm is frequently called Sollin's algorithm, especially in the parallel computing
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
literature.
The algorithm begins by first examining each vertex and adding the cheapest edge from that vertex to another in the graph, without regard to already added edges, and continues joining these groupings in a like manner until a tree spanning all vertices is completed.
Pseudocode
Designating each vertex or set of connected vertices a "component", pseudocode for Borůvka's algorithm is:1 Begin with a connected graph G containing edges of distinct weights, and an empty set of edges T
2 While the vertices of G connected by T are disjoint:
3 Begin with an empty set of edges E
4 For each component:
5 Begin with an empty set of edges S
6 For each vertex in the component:
7 Add the cheapest edge from the vertex in the component to another vertex in a disjoint component to S
8 Add the cheapest edge in S to E
9 Add the resulting set of edges E to T.
10 The resulting set of edges T is the minimum spanning tree of G.
Borůvka's algorithm can be shown to take O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(log V) iterations of the outer loop until it terminates, and therefore to run in time O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(Elog V), where E is the number of edges, and V is the number of vertices in G. In planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, and more generally in families of graphs closed under graph minor operations, it can be made to run in linear time, by removing all but the cheapest edge between each pair of components after each stage of the algorithm.
Other algorithms for this problem include Prim's algorithm
Prim's algorithm
In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
(actually discovered by Vojtěch Jarník
Vojtech Jarník
Vojtěch Jarník was a Czech mathematician.His main area of work was in number theory and mathematical analysis; he proved a number of results on lattice point problems. He also developed the graph theory algorithm known as Prim's algorithm....
) and Kruskal's algorithm
Kruskal's algorithm
Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
. Faster algorithms can be obtained by combining Prim's algorithm with Borůvka's. A faster randomized minimum spanning tree algorithm based in part on Borůvka's algorithm due to Karger, Klein, and Tarjan runs in expected
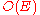time. The best known (deterministic) minimum spanning tree algorithm by Bernard ChazelleBernard Chazelle
Bernard Chazelle is the Eugene Higgins Professor of Computer Science at Princeton University. Much of his work is in computational geometry, where he has found many of the best-known algorithms, such as linear-time triangulation of a simple polygon, as well as many useful complexity results, such...
is also based in part on Borůvka's and runs in O(E α(V)) time, where α is the inverse of the Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
. These randomized and deterministic algorithms combine steps of Borůvka's algorithm, reducing the number of components that remain to be connected, with steps of a different type that reduce the number of edges between pairs of components.