
Boundedly generated group
Encyclopedia
In mathematics
, a group
is called boundedly generated if it can be expressed as a finite product of cyclic
subgroup
s. The property of bounded generation is also closely related with the congruence subgroup problem (see ).
The finite set S generates G, so a boundedly generated group is finitely generated.
An equivalent definition can be given in terms of cyclic subgroups. A group G is called boundedly generated if there is a finite family C1, …, CM of not necessarily distinct cyclic
subgroups such that G = C1…CM as a set.
A pseudocharacter on a discrete group G is defined to be a real-valued function f on a G such that
Since for any n ≥ 2, the free group
on 2 generators F2 contains the free group on n generators Fn as a subgroup of finite index (in fact n – 1), once one non-cyclic free group on finitely many generators is known to be not boundedly generated, this will be true for all of them. Similarly, since SL2(Z) contains F2 as a subgroup of index 12, it is enough to consider SL2(Z). In other words, to show that no Fn with n ≥ 2 has bounded generation, it is sufficient to prove this for one of them or even just for SL2(Z) .
will work. The existence of such groups constitutes Golod and Shafarevich
's negative solution of the generalized Burnside problem in 1964; later, other explicit examples of infinite finitely generated periodic groups were constructed by Aleshin, Olshanskii, and Grigorchuk, using automata
. Consequently, free groups of rank at least two are not boundedly generated.
Sn can be generated by two elements, a 2-cycle and an n-cycle, so that it is a quotient group of F2. On the other hand, it is easy to show that the maximal order M(n) of an element in Sn satisfies
(Edmund Landau
proved the more precise asymptotic estimate log M(n) ~ (n log n)1/2). In fact if the cycles in a cycle decomposition of a permutation
have length N1, ..., Nk with N1 + ··· + Nk = n, then the order of the permutation divides the product N1 ···Nk, which in turn is bounded by (n/k)k, using the inequality of arithmetic and geometric means
. On the other hand, (n/x)x is maximized when x=e. If F2 could be written as a product of m cyclic subgroups, then necessarily n! would have to be less than or equal to M(n)m for all n, contradicting Stirling's asymptotic formula
.
. Any compactly supported 1-form α on a fundamental domain
of G extends uniquely to a G-invariant 1-form on H. If z is in H and γ is the geodesic
from z to g(z), the function defined by

satisfies the first condition for a pseudocharacter since by the Stokes theorem
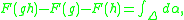
where Δ is the geodesic triangle with vertices z, g(z) and h−1(z), and geodesics triangles have area bounded by π. The homogenized function
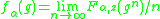
defines a pseudocharacter, depending only on α. As is well known from the theory of dynamical system
s, any orbit (gk(z)) of a hyperbolic element g has limit set consisting of two fixed points on the extended real axis; it follows that the geodesic segment from z to g(z) cuts through only finitely many translates of the fundamental domain. It is therefore easy to choose α so that fα equals one on a given hyperbolic element and vanishes on a finite set of other hyperbolic elements with distinct fixed points. Since G therefore has an infinite-dimensional space of pseudocharacters, it cannot be boundedly generated.
Dynamical properties of hyperbolic elements can similarly be used to prove that any non-elementary Gromov-hyperbolic group is not boundedly generated.
an infinite-dimensional family of pseudocharacters (see ). Epstein
and Fujiwara later extended these results to all non-elementary Gromov-hyperbolic groups.
proof uses dynamical properties of the action of hyperbolic elements on the Gromov boundary of a Gromov-hyperbolic group. For the special case of the free group Fn, the boundary (or space of ends) can be identified with the space X of semi-infinite
reduced words
in the generators and their inverses. It gives a natural compactification of the tree
, given by the Cayley graph
with respect to the generators. A sequence of semi-infinite words converges to another such word provided that the initial segments agree after a certain stage, so that X is compact (and metrizable). The free group acts by left multiplication on the semi-infinite words. Moreover any element g in Fn has exactly two fixed points g±∞, namely the reduced infinite words given by the limits of gn as n tends to ±∞. Furthermore gn·w tends to g±∞ as n tends to ±∞ for any semi-infinite word w; and more generally if wn tends to w≠ g ±∞, then gn·wn tends to g+∞ as n tends to ∞.
If Fn were boundedly generated, it could be written as a product of cyclic groups Ci
generated by elements hi. Let X0 be the countable subset given by the finitely many Fn-orbits
of the fixed points hi ±∞, the fixed points of the hi and all their conjugates. Since X is uncountable, there
is an element of g with fixed points outside X0 and a point w outside X0 different from these fixed points. Then for
some subsequence (gm) of (gn)
On the one hand, by successive use of the rules for computing limits of the form hn·wn, the limit of the right hand side applied to x is necessarily a fixed point of one of the conjugates of the hi's. On the other hand, this limit also must be g+∞, which is not one of these points, a contradiction.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is called boundedly generated if it can be expressed as a finite product of cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s. The property of bounded generation is also closely related with the congruence subgroup problem (see ).
Definitions
A group G is called boundedly generated if there exists a finite subset S of G and a positive integer m such that every element g of G can be represented as a product of at most m powers of the elements of S:-
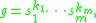 where
where 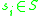 and
and  are integers.
are integers.
The finite set S generates G, so a boundedly generated group is finitely generated.
An equivalent definition can be given in terms of cyclic subgroups. A group G is called boundedly generated if there is a finite family C1, …, CM of not necessarily distinct cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
subgroups such that G = C1…CM as a set.
Properties
- Bounded generation is unaffected by passing to a subgroup of finite indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
: if H is a finite index subgroup of G then G is boundedly generated if and only if H is boundedly generated. - Any quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of a boundedly generated group is also boundedly generated. - A finitely generatedFinitely generatedIn mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
periodic groupPeriodic groupIn group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
must be finite if it is boundedly generated; equivalently, an infinite finitely generated periodic group is not boundedly generated.
A pseudocharacter on a discrete group G is defined to be a real-valued function f on a G such that
- f(gh) − f(g) − f(h) is uniformly bounded and f(gn) = n·f(g).
- The vector space of pseudocharacters of a boundedly generated group G is finite dimensional.
Examples
- If n ≥ 3, the group SLn(Z) is boundedly generated by its elementary subgroups, formed by matrices differing from the identity matrix only in one off-diagonal entry. In 1984, Carter and Keller gave an elementary proof of this result, motivated by a question in algebraic K-theoryAlgebraic K-theoryIn mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
. - A free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on at least two generators is not boundedly generated (see below). - The group SL2(Z) is not boundedly generated, since it contains a free subgroup with two generators of index 12.
- A Gromov-hyperbolic group is boundedly generated if and only if it is virtually cyclic (or elementary), i.e. contains a cyclic subgroup of finite index.
Free groups are not boundedly generated
Several authors have stated in the mathematical literature that it is obvious that finitely generated free groups are not boundedly generated. This section contains various obvious and less obvious ways of proving this. Some of the methods, which touch on bounded cohomology, are important because they are geometric rather than algebraic, so can be applied to a wider class of groups, for example Gromov-hyperbolic groups.Since for any n ≥ 2, the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on 2 generators F2 contains the free group on n generators Fn as a subgroup of finite index (in fact n – 1), once one non-cyclic free group on finitely many generators is known to be not boundedly generated, this will be true for all of them. Similarly, since SL2(Z) contains F2 as a subgroup of index 12, it is enough to consider SL2(Z). In other words, to show that no Fn with n ≥ 2 has bounded generation, it is sufficient to prove this for one of them or even just for SL2(Z) .
Burnside couterexamples
Since bounded generation is preserved under taking homomorphic images, if a single finitely generated group with at least two generators is known to be not boundedly generated, this will be true for the free group on the same number of generators, and hence for all free groups. To show that no (non-cyclic) free group has bounded generation, it is therefore enough to produce one example of a finitely generated group which is not boundedly generated, and any finitely generated infinite periodic groupPeriodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
will work. The existence of such groups constitutes Golod and Shafarevich
Golod–Shafarevich theorem
In mathematics, the Golod–Shafarevich theorem was proved in 1964 by two Russian mathematicians, Evgeny Golod and Igor Shafarevich. It is a result in non-commutative homological algebra which has consequences in various branches of algebra.-The inequality:...
's negative solution of the generalized Burnside problem in 1964; later, other explicit examples of infinite finitely generated periodic groups were constructed by Aleshin, Olshanskii, and Grigorchuk, using automata
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
. Consequently, free groups of rank at least two are not boundedly generated.
Symmetric groups
The symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn can be generated by two elements, a 2-cycle and an n-cycle, so that it is a quotient group of F2. On the other hand, it is easy to show that the maximal order M(n) of an element in Sn satisfies
- log M(n) ≤ n/e
(Edmund Landau
Edmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
proved the more precise asymptotic estimate log M(n) ~ (n log n)1/2). In fact if the cycles in a cycle decomposition of a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
have length N1, ..., Nk with N1 + ··· + Nk = n, then the order of the permutation divides the product N1 ···Nk, which in turn is bounded by (n/k)k, using the inequality of arithmetic and geometric means
Inequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
. On the other hand, (n/x)x is maximized when x=e. If F2 could be written as a product of m cyclic subgroups, then necessarily n! would have to be less than or equal to M(n)m for all n, contradicting Stirling's asymptotic formula
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
.
Hyperbolic geometry
There is also a simple geometric proof that that G = SL2(Z) is not boundedly generated. It acts by Möbius transformations on the upper half-plane H, with the Poincaré metricPoincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
. Any compactly supported 1-form α on a fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
of G extends uniquely to a G-invariant 1-form on H. If z is in H and γ is the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
from z to g(z), the function defined by

satisfies the first condition for a pseudocharacter since by the Stokes theorem
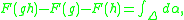
where Δ is the geodesic triangle with vertices z, g(z) and h−1(z), and geodesics triangles have area bounded by π. The homogenized function
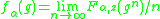
defines a pseudocharacter, depending only on α. As is well known from the theory of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, any orbit (gk(z)) of a hyperbolic element g has limit set consisting of two fixed points on the extended real axis; it follows that the geodesic segment from z to g(z) cuts through only finitely many translates of the fundamental domain. It is therefore easy to choose α so that fα equals one on a given hyperbolic element and vanishes on a finite set of other hyperbolic elements with distinct fixed points. Since G therefore has an infinite-dimensional space of pseudocharacters, it cannot be boundedly generated.
Dynamical properties of hyperbolic elements can similarly be used to prove that any non-elementary Gromov-hyperbolic group is not boundedly generated.
Brooks pseudocharacters
Robert Brooks gave a combinatorial scheme to produce pseudocharacters of any free group Fn; this scheme was later shown to yieldan infinite-dimensional family of pseudocharacters (see ). Epstein
David Epstein
David Epstein may refer to:* David Epstein , writer at Sports Illustrated* David B. A. Epstein , British mathematician* David G. Epstein, professor at the University of Richmond School of Law and bankruptcy expertSee also:...
and Fujiwara later extended these results to all non-elementary Gromov-hyperbolic groups.
Gromov boundary
This simple folkloreFolklore
Folklore consists of legends, music, oral history, proverbs, jokes, popular beliefs, fairy tales and customs that are the traditions of a culture, subculture, or group. It is also the set of practices through which those expressive genres are shared. The study of folklore is sometimes called...
proof uses dynamical properties of the action of hyperbolic elements on the Gromov boundary of a Gromov-hyperbolic group. For the special case of the free group Fn, the boundary (or space of ends) can be identified with the space X of semi-infinite
Semi-infinite
The term semi-infinite has several related meanings in various branches of pure and applied mathematics. It typically describes objects which are infinite or unbounded in some but not all possible ways.-In ordered structures and Euclidean spaces:...
reduced words
- g1 g2 ···
in the generators and their inverses. It gives a natural compactification of the tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, given by the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
with respect to the generators. A sequence of semi-infinite words converges to another such word provided that the initial segments agree after a certain stage, so that X is compact (and metrizable). The free group acts by left multiplication on the semi-infinite words. Moreover any element g in Fn has exactly two fixed points g±∞, namely the reduced infinite words given by the limits of gn as n tends to ±∞. Furthermore gn·w tends to g±∞ as n tends to ±∞ for any semi-infinite word w; and more generally if wn tends to w≠ g ±∞, then gn·wn tends to g+∞ as n tends to ∞.
If Fn were boundedly generated, it could be written as a product of cyclic groups Ci
generated by elements hi. Let X0 be the countable subset given by the finitely many Fn-orbits
of the fixed points hi ±∞, the fixed points of the hi and all their conjugates. Since X is uncountable, there
is an element of g with fixed points outside X0 and a point w outside X0 different from these fixed points. Then for
some subsequence (gm) of (gn)
- gm = h1n(m,1) ··· hkn(m,k), with each n(m,i) constant or strictly monotone.
On the one hand, by successive use of the rules for computing limits of the form hn·wn, the limit of the right hand side applied to x is necessarily a fixed point of one of the conjugates of the hi's. On the other hand, this limit also must be g+∞, which is not one of these points, a contradiction.

