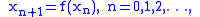Bourbaki–Witt theorem
Encyclopedia
In mathematics
, the Bourbaki–Witt theorem in order theory
, named after Nicolas Bourbaki
and Ernst Witt
, is a basic fixed point theorem for partially ordered set
s. It states that if X is a non-empty chain complete
poset, and
such that
then f has a fixed point
. Such a function f is called inflationary or progressive.
where x0 is any element of X, is monotone increasing. By the finiteness of X, it stabilizes:
It follows that x∞ is a fixed point of f.
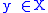 . Define a function K recursively on the ordinals as follows:
. Define a function K recursively on the ordinals as follows:
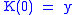

If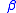 is a limit ordinal, then by construction
is a limit ordinal, then by construction

is a chain in X. Define
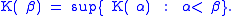
This is now an increasing function from the ordinals into X. It cannot be strictly increasing, as if it were we would have an injective function
from the ordinals into a set, violating Hartogs' lemma
. Therefore the function must be eventually constant, so for some
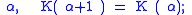
that is,

So letting
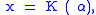
we have our desired fixed point. Q.E.D.
. We first prove it for the case where X is chain complete and has no maximal element. Let g be a choice function on

Define a function

by
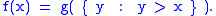
This is allowed as, by assumption, the set is non-empty. Then f(x) > x, so f is an inflationary function with no fixed point, contradicting the theorem.
This special case of Zorn's lemma is then used to prove the Hausdorff maximality principle, that every poset has a maximal chain, which is easily seen to be equivalent to Zorn's Lemma.
Bourbaki–Witt has other applications. In particular in computer science
, it is used in the theory of computable function
s.
It is also used to define recursive data types, e.g. linked lists, in domain theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bourbaki–Witt theorem in order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, named after Nicolas Bourbaki
Nicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
and Ernst Witt
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
, is a basic fixed point theorem for partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s. It states that if X is a non-empty chain complete
Chain complete
In mathematics, a partially ordered set in order theory is chain complete if every chain in it has a least upper bound.Unlike complete posets, chain complete posets are relatively common...
poset, and
such that
-
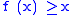 for all
for all 
then f has a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
. Such a function f is called inflationary or progressive.
Special case of a finite poset
If the poset X is finite then the statement of the theorem has a clear interpretation that leads to the proof. The sequence of successive iterates,where x0 is any element of X, is monotone increasing. By the finiteness of X, it stabilizes:
-
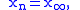 for n sufficiently large.
for n sufficiently large.
It follows that x∞ is a fixed point of f.
Proof of the theorem
Pick some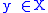 . Define a function K recursively on the ordinals as follows:
. Define a function K recursively on the ordinals as follows: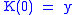

If
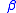 is a limit ordinal, then by construction
is a limit ordinal, then by construction
is a chain in X. Define
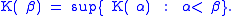
This is now an increasing function from the ordinals into X. It cannot be strictly increasing, as if it were we would have an injective function
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from the ordinals into a set, violating Hartogs' lemma
Hartogs number
In mathematics, specifically in axiomatic set theory, a Hartogs number is a particular kind of cardinal number. It was shown by Friedrich Hartogs in 1915, from ZF alone , that there is a least well-ordered cardinal greater than a given well-ordered cardinal.To define the Hartogs number of a set it...
. Therefore the function must be eventually constant, so for some
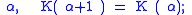
that is,

So letting
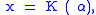
we have our desired fixed point. Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
Applications
The Bourbaki–Witt theorem has various important applications. One of the most common is in the proof that the axiom of choice implies Zorn's lemmaZorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
. We first prove it for the case where X is chain complete and has no maximal element. Let g be a choice function on

Define a function

by
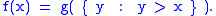
This is allowed as, by assumption, the set is non-empty. Then f(x) > x, so f is an inflationary function with no fixed point, contradicting the theorem.
This special case of Zorn's lemma is then used to prove the Hausdorff maximality principle, that every poset has a maximal chain, which is easily seen to be equivalent to Zorn's Lemma.
Bourbaki–Witt has other applications. In particular in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, it is used in the theory of computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s.
It is also used to define recursive data types, e.g. linked lists, in domain theory
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
.