Braess' paradox
Encyclopedia
Braess's paradox, credited to the mathematician Dietrich Braess, states that adding extra capacity to a network when the moving entities selfishly choose their route, can in some cases reduce overall performance. This is because the Nash equilibrium
of such a system is not necessarily optimal.
The paradox is stated as follows: "For each point of a road network, let there be given the number of cars starting from it, and the destination of the cars. Under these conditions one wishes to estimate the distribution of traffic flow. Whether one street is preferable to another depends not only on the quality of the road, but also on the density of the flow. If every driver takes the path that looks most favorable to him, the resultant running times need not be minimal. Furthermore, it is indicated by an example that an extension of the road network may cause a redistribution of the traffic that results in longer individual running times."
The reason for this is that in a Nash equilibrium, drivers have no incentive to change their routes. If the system is not in a Nash equilibrium, selfish drivers must be able to improve their respective travel times by changing the routes they take. In the case of Braess's paradox, drivers will continue to switch until they reach Nash equilibrium, despite the reduction in overall performance.
If the latency functions are linear then adding an edge can never make total travel time at equilibrium worse by a factor of more than 4/3.
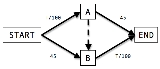
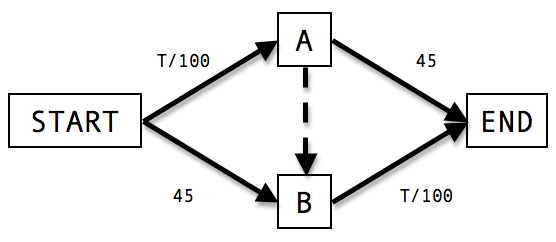Consider a road network as shown in the adjacent diagram, on which 4000 drivers wish to travel from point Start to End. The travel time in minutes on the Start-A road is the number of travelers (T) divided by 100, and on Start-B is a constant 45 minutes (likewise with the roads across from them). If the dashed road does not exist (so the traffic network has 4 roads in total), the time needed to drive Start-A-End route with A drivers would be 
. And the time needed to drive the Start-B-End route with B drivers would be 
. If either route were shorter, it would not be a Nash equilibrium: a rational driver would switch routes from the longer route to the shorter route. As there are 4000 drivers, the fact that 
can be used to derive the fact that 
when the system is at equilibrium. Therefore, each route takes 
minutes.
Now suppose the dashed line is a road with an extremely short travel time of approximately 0 minutes. In this situation, all drivers will choose the Start-A route rather than the Start-B route, because Start-A will only take
minutes at its worst, whereas Start-B is guaranteed to take 45 minutes. Once at point A, every rational driver will elect to take the "free" road to B and from there continue to End, because once again A-End is guaranteed to take 45 minutes while A-B-End will take at most 
minutes. Each driver's travel time is 
minutes, an increase from the 65 minutes required when the fast A-B road did not exist. No driver has an incentive to switch, as the two original routes (Start-A-End and Start-B-End) are both now 85 minutes. If every driver were to agree not to use the A-B path, every driver would benefit by reducing their travel time by 15 minutes. However, because any single driver will always benefit by taking the A-B path, the socially optimal distribution is not stable and so Braess's paradox occurs.
be the formula for the cost of 
people driving along edge 
. If a traffic graph has linear edges (those of the form 
where 
and 
are constants) then an equilibrium will always exist.
Suppose we have a linear traffic graph with
people driving along edge 
. Let the energy of e, 
be
(If
let 
). Let the total energy of the traffic graph be the sum of the energies of every edge in the graph.
Suppose that the distribution for the traffic graph is not an equilibrium. There must be at least one driver who can switch their route and improve total travel time. Suppose their original route is
while their new route is 
. Let 
be total energy of the traffic graph, and consider what happens when the route 
is removed. The energy of each edge 
will be reduced by 
and so the 
will be reduced by 
. Note that this is simply the total travel time needed to take the original route. If we then add the new route, 
, 
will be increased by the total travel time needed to take the new route. Because the new route is shorter than the original route, 
must decrease. If we repeat this process, 
will continue to decrease. As 
must remain positive, eventually an equilibrium must occur.
, which finds an equilibrium for a linear traffic graph and terminates in a finite number of steps. The algorithm is termed "best response" because at each step of the algorithm, if the graph is not at equilibrium then some driver has a best response to the strategies of all other drivers, and switches to that response.
Pseudocode for Best Response Dynamics:
Let P be some traffic pattern.
while P is not at equilibrium:
compute the potential energy e of P
for each driver d in P:
for each alternate path p available to d:
compute the potential energy n of the pattern when d takes path p
if n < e:
modify P so that d takes path p
continue the topmost while
At each step, if some particular driver could do better by taking an alternate path (a "best response"), doing so strictly decreases the energy of the graph. If no driver has a best response, the graph is at equilibrium. Since the energy of the graph strictly decreases with each step, the Best Response Dynamics algorithm must eventually halt.
Proof
= starting point for car j
= target for car j
Strategies for car j are possible paths from
to 
Each edge e has a travel function
for some 
Energy on edge e with x drivers:
Total time spent by all drivers on that edge:
((where there are x terms))
E(e) is less than or equal to T(e)
Resulting Inequality
If Z is a traffic pattern:
If we start from a socially optimal traffic pattern Z and end in an equilibrium pattern Z':
Thus we can see that worst is twice as bad as optimal.
In Seoul
, South Korea
, a speeding-up in traffic around the city was seen when a motorway was removed as part of the Cheonggyecheon
restoration project. In Stuttgart
, Germany
after investments into the road network in 1969, the traffic situation did not improve until a section of newly-built road was closed for traffic again. In 1990 the closing of 42nd street in New York City
reduced the amount of congestion in the area. In 2008 Youn, Gastner and Jeong demonstrated specific routes in Boston, New York City and London where this might actually occur and pointed out roads that could be closed to reduce predicted travel times.
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
of such a system is not necessarily optimal.
The paradox is stated as follows: "For each point of a road network, let there be given the number of cars starting from it, and the destination of the cars. Under these conditions one wishes to estimate the distribution of traffic flow. Whether one street is preferable to another depends not only on the quality of the road, but also on the density of the flow. If every driver takes the path that looks most favorable to him, the resultant running times need not be minimal. Furthermore, it is indicated by an example that an extension of the road network may cause a redistribution of the traffic that results in longer individual running times."
The reason for this is that in a Nash equilibrium, drivers have no incentive to change their routes. If the system is not in a Nash equilibrium, selfish drivers must be able to improve their respective travel times by changing the routes they take. In the case of Braess's paradox, drivers will continue to switch until they reach Nash equilibrium, despite the reduction in overall performance.
If the latency functions are linear then adding an edge can never make total travel time at equilibrium worse by a factor of more than 4/3.
Example
. And the time needed to drive the Start-B-End route with B drivers would be . If either route were shorter, it would not be a Nash equilibrium: a rational driver would switch routes from the longer route to the shorter route. As there are 4000 drivers, the fact that can be used to derive the fact that when the system is at equilibrium. Therefore, each route takes minutes.Now suppose the dashed line is a road with an extremely short travel time of approximately 0 minutes. In this situation, all drivers will choose the Start-A route rather than the Start-B route, because Start-A will only take
minutes at its worst, whereas Start-B is guaranteed to take 45 minutes. Once at point A, every rational driver will elect to take the "free" road to B and from there continue to End, because once again A-End is guaranteed to take 45 minutes while A-B-End will take at most minutes. Each driver's travel time is minutes, an increase from the 65 minutes required when the fast A-B road did not exist. No driver has an incentive to switch, as the two original routes (Start-A-End and Start-B-End) are both now 85 minutes. If every driver were to agree not to use the A-B path, every driver would benefit by reducing their travel time by 15 minutes. However, because any single driver will always benefit by taking the A-B path, the socially optimal distribution is not stable and so Braess's paradox occurs.Existence of an equilibrium
Let be the formula for the cost of people driving along edge . If a traffic graph has linear edges (those of the form where and are constants) then an equilibrium will always exist.Suppose we have a linear traffic graph with
people driving along edge . Let the energy of e, be
(If
let ). Let the total energy of the traffic graph be the sum of the energies of every edge in the graph.Suppose that the distribution for the traffic graph is not an equilibrium. There must be at least one driver who can switch their route and improve total travel time. Suppose their original route is
while their new route is . Let be total energy of the traffic graph, and consider what happens when the route is removed. The energy of each edge will be reduced by and so the will be reduced by . Note that this is simply the total travel time needed to take the original route. If we then add the new route, , will be increased by the total travel time needed to take the new route. Because the new route is shorter than the original route, must decrease. If we repeat this process, will continue to decrease. As must remain positive, eventually an equilibrium must occur.Finding an equilibrium
The above proof outlines a procedure known as Best Response DynamicsBest response
In game theory, the best response is the strategy which produces the most favorable outcome for a player, taking other players' strategies as given...
, which finds an equilibrium for a linear traffic graph and terminates in a finite number of steps. The algorithm is termed "best response" because at each step of the algorithm, if the graph is not at equilibrium then some driver has a best response to the strategies of all other drivers, and switches to that response.
Pseudocode for Best Response Dynamics:
Let P be some traffic pattern.
while P is not at equilibrium:
compute the potential energy e of P
for each driver d in P:
for each alternate path p available to d:
compute the potential energy n of the pattern when d takes path p
if n < e:
modify P so that d takes path p
continue the topmost while
At each step, if some particular driver could do better by taking an alternate path (a "best response"), doing so strictly decreases the energy of the graph. If no driver has a best response, the graph is at equilibrium. Since the energy of the graph strictly decreases with each step, the Best Response Dynamics algorithm must eventually halt.
How far from optimal is traffic at equilibrium
At worst, traffic in equilibrium is twice as bad as socially optimalProof
= starting point for car j = target for car jStrategies for car j are possible paths from
to Each edge e has a travel function
for some Energy on edge e with x drivers:
Total time spent by all drivers on that edge:
((where there are x terms))E(e) is less than or equal to T(e)
Resulting Inequality
If Z is a traffic pattern:
If we start from a socially optimal traffic pattern Z and end in an equilibrium pattern Z':
Thus we can see that worst is twice as bad as optimal.
How rare is Braess's paradox?
In 1983 Steinberg and Zangwill provided, under reasonable assumptions, necessary and sufficient conditions for Braess's paradox to occur in a general transportation network when a new route is added. (Note that their result applies to the addition of any new route — not just to the case of adding a single link.) As a corollary, they obtain that Braess's paradox is about as likely to occur as not occur; their result applies to random rather than planned networks and additions.In Seoul
Seoul
Seoul , officially the Seoul Special City, is the capital and largest metropolis of South Korea. A megacity with a population of over 10 million, it is the largest city proper in the OECD developed world...
, South Korea
South Korea
The Republic of Korea , , is a sovereign state in East Asia, located on the southern portion of the Korean Peninsula. It is neighbored by the People's Republic of China to the west, Japan to the east, North Korea to the north, and the East China Sea and Republic of China to the south...
, a speeding-up in traffic around the city was seen when a motorway was removed as part of the Cheonggyecheon
Cheonggyecheon
Cheonggyecheon is an 8.4 km long, modern public recreation space in downtown Seoul, South Korea. The massive urban renewal project is on the site of a stream that flowed before the rapid post-war economic development required it to be covered by transportation infrastructure...
restoration project. In Stuttgart
Stuttgart
Stuttgart is the capital of the state of Baden-Württemberg in southern Germany. The sixth-largest city in Germany, Stuttgart has a population of 600,038 while the metropolitan area has a population of 5.3 million ....
, Germany
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
after investments into the road network in 1969, the traffic situation did not improve until a section of newly-built road was closed for traffic again. In 1990 the closing of 42nd street in New York City
New York City
New York is the most populous city in the United States and the center of the New York Metropolitan Area, one of the most populous metropolitan areas in the world. New York exerts a significant impact upon global commerce, finance, media, art, fashion, research, technology, education, and...
reduced the amount of congestion in the area. In 2008 Youn, Gastner and Jeong demonstrated specific routes in Boston, New York City and London where this might actually occur and pointed out roads that could be closed to reduce predicted travel times.
See also
- Downs-Thomson paradoxDowns-Thomson paradoxDowns-Thomson paradox , also referred to as the Pigou–Knight–Downs paradox , states that the equilibrium speed of car traffic on the road network is determined by the average door-to-door speed of equivalent journeys by public transport.It follows that increasing...
- Belady's anomalyBelady's anomalyIn computer storage, Bélády's anomaly proves that it is possible to have more page faults when increasing the number of page frames while using the First in First Out page replacement algorithm. László Bélády demonstrated this in 1969....
- Paradox of enrichmentParadox of enrichmentThe paradox of enrichment is a term from population ecology coined by Michael Rosenzweig in 1971. He described an effect in six predator-prey models wherein increasing the food available to the prey caused the predator's population to destabilize...
: Increasing the food available to an ecosystem may introduce dynamic instability, and even lead to extinction. - Induced demandInduced demandInduced demand, or latent demand, is the phenomenon that after supply increases, more of a good is consumed. This is entirely consistent with the economic theory of supply and demand; however, this idea has become important in the debate over the expansion of transportation systems, and is often...
- Lewis-Mogridge PositionLewis-Mogridge PositionThe Lewis–Mogridge Position, named after D. Lewis and M. J. H. Mogridge, was formulated in 1990. It captures the observation that the more roads are built, the more traffic there is to fill these roads. Speed gains from some new roads can disappear within months if not weeks...
- Traffic waveTraffic waveTraffic waves, also called stop waves or traffic shocks, are travelling disturbances in the distribution of cars on a highway. Traffic waves usually travel backwards in relation to the motion of the cars themselves, or "upstream". The waves can also travel downstream, however, more commonly become...
Further reading
- D. Braess, Über ein Paradoxon aus der Verkehrsplanung. Unternehmensforschung 12, 258–268 (1969) http://homepage.ruhr-uni-bochum.de/Dietrich.Braess/paradox.pdf http://homepage.rub.de/Dietrich.Braess/Paradox-BNW.pdf
- Katharina Belaga-Werbitzky: „Das Paradoxon von Braess in erweiterten Wheatstone-Netzen mit M/M/1-Bedienern“ ISBN 3-89959-123-2
- Translation of the Braess 1968 article from German to English appears as the article "On a paradox of traffic planning," by D. Braess, A. Nagurney, and T. Wakolbinger in the journal Transportation Science, volume 39, 2005, pp. 446–450. More information
- A. D. Irvine. How Braess's Paradox Solves Newcomb's Problem. International Studies in Philosophy of Science, Vol. 7 (1993), no. 2, 145–164.
- R. Steinberg and W.I. Zangwill. The Prevalence of Braess's Paradox. Transportation Science, Vol. 17 (1983), no. 3, 301–318.
- A. Rapoport, T. Kugler, S. Dugar, and E. J. Gisches, Choice of routes in congested traffic networks: Experimental tests of the Braess Paradox. Games and Economic Behavior 65 (2009) http://www.parisschoolofeconomics.eu/IMG/pdf/Choices_of_routes.pdf
- T. Roughgarden. "The Price of Anarchy." MIT Press, Cambridge, MA, 2005.