Paradox of enrichment
Encyclopedia
The paradox of enrichment is a term from population ecology
coined by Michael Rosenzweig
in 1971. He described an effect in six predator-prey models wherein increasing the food available to the prey caused the predator's population to destabilize. A common example is that if the food supply of a prey such as a rabbit is overabundant, its population will grow unbounded and cause the predator population (such as a lynx) to grow unsustainably large. This may result in a crash in the population of the predators and possibly lead to local eradication or even species extinction.
The term 'paradox' has been used since then to describe this effect in slightly conflicting ways. The original sense was one of irony; that by attempting to increase carrying capacity in an ecosystem, one could fatally imbalance it. Since then, some authors have used the word to describe the difference between modelled and real predator-prey interactions.
models to simulate the prey population. Models only represented prey populations. Enrichment was taken to be increasing the prey carrying capacity
and showing that the prey population destabilized, usually into a limit cycle.
The cycling behavior after destabilization was more thoroughly explored in a subsequent paper (May 1972) and discussion (Gilpin and Rozenzweig 1972).
. As the carrying capacity
increases, the equilibrium of the dynamical system
becomes unstable.
The bifurcation can be obtained by modifying the Lotka-Volterra equation
. First, one assumes that the growth of the prey population is determined by the logistic equation. Second, one assumes that predators have a non-linear functional response
, typically of type II. The saturation in consumption may be caused by the time to handle the prey or satiety effects.
Thus, one can write the following (normalized) equations:
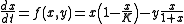
The term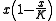
represents the prey's logistic growth, and 
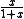the predator's functional response.
The prey isocline
s (points at which the prey population does not change, i.e. dx/dt = 0) are easily obtained as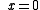
and 
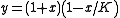. Likewise, the predator isoclines are obtained as 
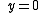and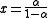 
, where 
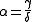. The intersections of the isoclines yields three equilibrium states:
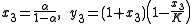
The first equilibrium corresponds to the extinction of both predator and prey, the second one to the extinction of the predator, and the third to co-existence.
The standard method to determine the stability of the steady states is to approximate the non-linear system by a linear system which can be solved in closed form. After differentiating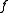
and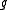 
with respect to 
and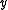 
in a neighborhood of 
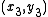, we get:
It is possible to find the exact solution of this linear system, but here, we are only interested in the qualitative behavior. It is a classical result of linear systems that if both eigenvalues of the matrix are real and negative, the system converges to a limit point. Since the determinant is equal to the product of the eigenvalues and is positive, both eigenvalues have the same sign. Since the trace is equal to the sum of the eigenvalues, the system is stable if:
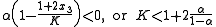
At this critical value of the parameter K, the system undergoes a Hopf bifurcation
. This comes as counter-intuitive (hence the term 'paradox') because increasing the carrying capacity of the ecological system beyond a certain value leads to dynamic instability, and extinction of the predator species.
Population ecology
Population ecology is a sub-field of ecology that deals with the dynamics of species populations and how these populations interact with the environment. It is the study of how the population sizes of species living together in groups change over time and space....
coined by Michael Rosenzweig
Michael Rosenzweig
Michael L. Rosenzweig is an ecologist at the University of Arizona who has developed and popularized the concept of Reconciliation ecology. He founded and developed the Department of Ecology and Evolutionary Biology, at UA Tucson, now a major center for the study of Evolutionary Ecology...
in 1971. He described an effect in six predator-prey models wherein increasing the food available to the prey caused the predator's population to destabilize. A common example is that if the food supply of a prey such as a rabbit is overabundant, its population will grow unbounded and cause the predator population (such as a lynx) to grow unsustainably large. This may result in a crash in the population of the predators and possibly lead to local eradication or even species extinction.
The term 'paradox' has been used since then to describe this effect in slightly conflicting ways. The original sense was one of irony; that by attempting to increase carrying capacity in an ecosystem, one could fatally imbalance it. Since then, some authors have used the word to describe the difference between modelled and real predator-prey interactions.
Rosenzweig's result (Rosenzweig 1971)
Rosenzweig used ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
models to simulate the prey population. Models only represented prey populations. Enrichment was taken to be increasing the prey carrying capacity
Carrying capacity
The carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
and showing that the prey population destabilized, usually into a limit cycle.
The cycling behavior after destabilization was more thoroughly explored in a subsequent paper (May 1972) and discussion (Gilpin and Rozenzweig 1972).
Model and Exception
Many studies have been done on the paradox of enrichment since Rosenzweig, and some have shown that the model initially proposed does not hold in all circumstances, as summarised by Roy and Chattopadhyay in 2007. Cases where the paradox of enrichment may not apply include the following:- inedible prey: if there are multiple prey species, and not all are edible, then some may absorb nutrients and stabilise cyclicity.
- invulnerable prey: even with a single prey species, if there is a degree of temporal or spatial refuge (i.e. the prey can hide from the predator), then destabilisation may not happen
- unpalatable prey: if prey do not fulfil the nutritional preferences of the predator to as great an extent at higher densities, as with some algae and grazers, then there may be a stabilising effect
- heterogeneous environment: the model for enrichment follows an assumption of environmental homogeneity. If a spatiotemporally chaotic, heterogeneous environment is introduced, then cyclic patterns may not arise
- induced defense: if there is a predation-dependent response from prey species, then it may act to decelerate the downward swing of population caused by the boom in predator population. An example is of DaphniaDaphniaDaphnia are small, planktonic crustaceans, between 0.2 and 5 mm in length. Daphnia are members of the order Cladocera, and are one of the several small aquatic crustaceans commonly called water fleas because of their saltatory swimming style...
and fish predators. - autotoxins and other predator density-dependent effects: If predator density cannot increase in proportion to that of prey, then destabilising periodicities may not develop.
- prey toxicity: if there is a significant cost to the predator of consuming the (now highly-dense) prey species, then predator numbers may not increase sufficiently to give periodicity
Link with the Hopf bifurcation
The paradox of enrichment can be accounted for by the bifurcation theoryBifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
. As the carrying capacity
Carrying capacity
The carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
increases, the equilibrium of the dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
becomes unstable.
The bifurcation can be obtained by modifying the Lotka-Volterra equation
Lotka-Volterra equation
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order, non-linear, differential equations frequently used to describe the dynamics of biological systems in which two species interact, one a predator and one its prey...
. First, one assumes that the growth of the prey population is determined by the logistic equation. Second, one assumes that predators have a non-linear functional response
Functional response
A functional response in ecology is the intake rate of a consumer as a function of food density. It is associated with the numerical response, which is the reproduction rate of a consumer as a function of food density. Following C. S...
, typically of type II. The saturation in consumption may be caused by the time to handle the prey or satiety effects.
Thus, one can write the following (normalized) equations:
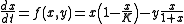
- x is the prey density;
- y is the predator density;
- K is the prey population's carrying capacityCarrying capacityThe carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
; - γ and δ are predator population's parameters (rate of decay and benefits of consumption, respectively).
The term
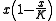represents the prey's logistic growth, and 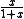the predator's functional response.The prey isocline
Isocline
thumb|right|300px|Fig. 1: Isoclines , slope field , and some solution curves of y'=xyAn Isocline is a curve through points at which the parent function's slope will always be the same, regardless of initial conditions...
s (points at which the prey population does not change, i.e. dx/dt = 0) are easily obtained as
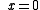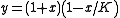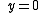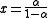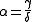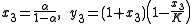
and . Likewise, the predator isoclines are obtained as and , where . The intersections of the isoclines yields three equilibrium states:The first equilibrium corresponds to the extinction of both predator and prey, the second one to the extinction of the predator, and the third to co-existence.
The standard method to determine the stability of the steady states is to approximate the non-linear system by a linear system which can be solved in closed form. After differentiating
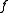and 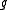with respect to and 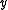in a neighborhood of 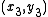, we get:It is possible to find the exact solution of this linear system, but here, we are only interested in the qualitative behavior. It is a classical result of linear systems that if both eigenvalues of the matrix are real and negative, the system converges to a limit point. Since the determinant is equal to the product of the eigenvalues and is positive, both eigenvalues have the same sign. Since the trace is equal to the sum of the eigenvalues, the system is stable if:
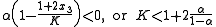
At this critical value of the parameter K, the system undergoes a Hopf bifurcation
Hopf bifurcation
In the mathematical theory of bifurcations, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf, and Aleksandr Andronov, is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of...
. This comes as counter-intuitive (hence the term 'paradox') because increasing the carrying capacity of the ecological system beyond a certain value leads to dynamic instability, and extinction of the predator species.
See also
- Braess's paradox: Adding extra capacity to a network may reduce overall performance.
- Paradox of the pesticidesParadox of the pesticidesThe paradox of the pesticides is a paradox that states that by applying pesticide to a pest, one may in fact increase its abundance. This happens when the pesticide upsets natural predator-prey dynamics in the ecosystem....
: Applying pesticide may increase the pest population.