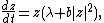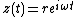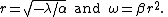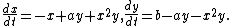Hopf bifurcation
Encyclopedia
In the mathematical theory of bifurcations
, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré
, Eberhard Hopf
, and Aleksandr Andronov, is a local bifurcation in which a fixed point
of a dynamical system
loses stability as a pair of complex conjugate
eigenvalues of the linearization
around the fixed point cross the imaginary axis of the complex plane
. Under reasonably generic assumptions about the dynamical system, we can expect to see a small-amplitude limit cycle branching from the fixed point.
For a more general survey on Hopf bifurcation and dynamical systems in general, see .
The normal form of a Hopf bifurcation is:
where z, b are both complex and λ is a parameter. Write
The number α is called the first Lyapunov coefficient.
Under some general hypothesis, in the neighborhood of a Hopf bifurcation, a stable steady point
of the system gives birth to a small stable limit cycle. Remark that looking for Hopf bifurcation is not equivalent to looking for stable limit cycles. First, some Hopf bifurcations (e.g. subcritical ones) do not imply the existence of stable limit cycles; second, there may exist limit cycles not related to Hopf bifurcations.
 Hopf bifurcations occur in the Hodgkin–Huxley model for nerve membrane (no citation), the Selkov model of glycolysis
Hopf bifurcations occur in the Hodgkin–Huxley model for nerve membrane (no citation), the Selkov model of glycolysis
, the Belousov–Zhabotinsky reaction, the Lorenz attractor
and in the following simpler chemical system called the Brusselator
as the parameter B changes:
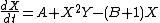
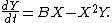
The Selkov model is
The phase portrait illustrating the Hopf bifurcation in the Selkov model is shown on the right. See Strogatz, Steven H. (1994). "Nonlinear Dynamics and Chaos" , page 205 for detailed derivation.
Theorem (see section 11.2 of ). Let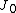 be the Jacobian
be the Jacobian
of a continuous parametric dynamical system
evaluated at a steady point of it. Suppose that all eigenvalues of
of it. Suppose that all eigenvalues of 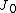 have negative real parts except one conjugate nonzero purely imaginary pair
have negative real parts except one conjugate nonzero purely imaginary pair 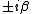 . A Hopf bifurcation arises when these two eigenvalues cross the imaginary axis because of a variation of the system parameters.
. A Hopf bifurcation arises when these two eigenvalues cross the imaginary axis because of a variation of the system parameters.
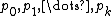 be Sturm series
be Sturm series
associated to a characteristic polynomial
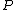 . They can be written in the form:
. They can be written in the form:
The coefficients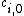 for
for 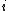 in
in  correspond to what is called Hurwitz determinants. Their definition is related to the associated Hurwitz matrix
correspond to what is called Hurwitz determinants. Their definition is related to the associated Hurwitz matrix
.
 are positive, apart perhaps
are positive, apart perhaps  then the associated Jacobian has no pure imaginary eigenvalues.
then the associated Jacobian has no pure imaginary eigenvalues.
Proposition 2. If all Hurwitz determinants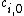 (for all
(for all 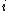 in
in 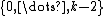 are positive,
are positive,  and
and 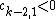 then all the eigenvalues of the associated Jacobian have negative real parts except a purely imaginary conjugate pair.
then all the eigenvalues of the associated Jacobian have negative real parts except a purely imaginary conjugate pair.
The conditions that we are looking for so that a Hopf bifurcation occurs (see theorem above) for a parametric continuous dynamical system are given by this last proposition.
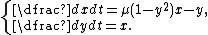
The Jacobian matrix associated to this system follows:
The characteristic polynomial (in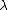 ) of the linearization at (0,0) is equal to:
) of the linearization at (0,0) is equal to: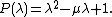
The coefficients are:
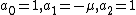
The associated Sturm series
is: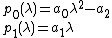
The Sturm
polynomials can be written as (here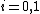 ):
):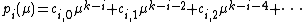
The above proposition 2 tells that one must have: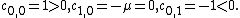
Because 1 > 0 and −1 < 0 are obvious, one can conclude that a Hopf bifurcation may occur for Van der Pol oscillator if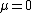 .
.
Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, Eberhard Hopf
Eberhard Hopf
Eberhard Frederich Ferdinand Hopf was a mathematician and astronomer, one of the founding fathers of ergodic theory and a pioneer of bifurcation theory who also made significant contributions to the subjects of partial differential equations and integral equations, fluid dynamics, and differential...
, and Aleksandr Andronov, is a local bifurcation in which a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
loses stability as a pair of complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
eigenvalues of the linearization
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
around the fixed point cross the imaginary axis of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. Under reasonably generic assumptions about the dynamical system, we can expect to see a small-amplitude limit cycle branching from the fixed point.
For a more general survey on Hopf bifurcation and dynamical systems in general, see .
Supercritical / subcritical Hopf bifurcations
The limit cycle is orbitally stable if a certain quantity called the first Lyapunov coefficient is negative, and the bifurcation is supercritical. Otherwise it is unstable and the bifurcation is subcritical.The normal form of a Hopf bifurcation is:
where z, b are both complex and λ is a parameter. Write
The number α is called the first Lyapunov coefficient.
- If α is negative then there is a stable limit cycle for λ > 0:
-
- where
- The bifurcation is then called supercritical.
- If α is positive then there is an unstable limit cycle for λ < 0. The bifurcation is called subcritical.
Remarks
The "smallest chemical reaction with Hopf bifurcation" was found in 1995 in Berlin, Germany. The same biochemical system has been used in order to investigate how the existence of a Hopf bifurcation influences our ability to reverse-engineer dynamical systems.Under some general hypothesis, in the neighborhood of a Hopf bifurcation, a stable steady point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of the system gives birth to a small stable limit cycle. Remark that looking for Hopf bifurcation is not equivalent to looking for stable limit cycles. First, some Hopf bifurcations (e.g. subcritical ones) do not imply the existence of stable limit cycles; second, there may exist limit cycles not related to Hopf bifurcations.
Example

Glycolysis
Glycolysis is the metabolic pathway that converts glucose C6H12O6, into pyruvate, CH3COCOO− + H+...
, the Belousov–Zhabotinsky reaction, the Lorenz attractor
Lorenz attractor
The Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...
and in the following simpler chemical system called the Brusselator
Brusselator
[Image:080205 Brusselator picture.jpg|thumb|right|350px|The Brusselator in the unstable regime. A=1. B=2.5. X=1. Y=0. The system approaches a limit cycle For B1+A^2 \,...
as the parameter B changes:
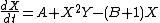
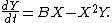
The Selkov model is
The phase portrait illustrating the Hopf bifurcation in the Selkov model is shown on the right. See Strogatz, Steven H. (1994). "Nonlinear Dynamics and Chaos" , page 205 for detailed derivation.
Definition of a Hopf bifurcation
The appearance or the disappearance of a periodic orbit through a local change in the stability properties of a steady point is known as the Hopf bifurcation. The following theorem works with steady points with one pair of conjugate nonzero purely imaginary eigenvalues. It tells the conditions under which this bifurcation phenomenon occurs.Theorem (see section 11.2 of ). Let
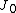 be the Jacobian
be the JacobianJacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of a continuous parametric dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
evaluated at a steady point
 of it. Suppose that all eigenvalues of
of it. Suppose that all eigenvalues of 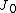 have negative real parts except one conjugate nonzero purely imaginary pair
have negative real parts except one conjugate nonzero purely imaginary pair 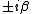 . A Hopf bifurcation arises when these two eigenvalues cross the imaginary axis because of a variation of the system parameters.
. A Hopf bifurcation arises when these two eigenvalues cross the imaginary axis because of a variation of the system parameters.Routh–Hurwitz criterion
Routh–Hurwitz criterion (section I.13 of ) gives necessary conditions so that a Hopf bifurcation occurs. Let us see how one can use concretely this idea.Sturm series
Let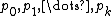 be Sturm series
be Sturm seriesSturm series
In mathematics, the Sturm series associated with a pair of polynomials is named after Jacques Charles François Sturm.-Definition:Let p_0 and p_1 two univariate polynomials. Suppose that they do not have a common root and the degree of p_0 is greater than the degree of p_1...
associated to a characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
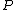 . They can be written in the form:
. They can be written in the form:
The coefficients
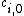 for
for 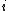 in
in  correspond to what is called Hurwitz determinants. Their definition is related to the associated Hurwitz matrix
correspond to what is called Hurwitz determinants. Their definition is related to the associated Hurwitz matrixHurwitz matrix
-Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial...
.
Propositions
Proposition 1. If all the Hurwitz determinants are positive, apart perhaps
are positive, apart perhaps  then the associated Jacobian has no pure imaginary eigenvalues.
then the associated Jacobian has no pure imaginary eigenvalues.Proposition 2. If all Hurwitz determinants
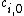 (for all
(for all 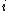 in
in 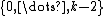 are positive,
are positive,  and
and 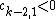 then all the eigenvalues of the associated Jacobian have negative real parts except a purely imaginary conjugate pair.
then all the eigenvalues of the associated Jacobian have negative real parts except a purely imaginary conjugate pair.The conditions that we are looking for so that a Hopf bifurcation occurs (see theorem above) for a parametric continuous dynamical system are given by this last proposition.
Example
Let us consider the classical Van der Pol oscillator written with ordinary differential equations: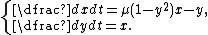
The Jacobian matrix associated to this system follows:

The characteristic polynomial (in
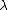 ) of the linearization at (0,0) is equal to:
) of the linearization at (0,0) is equal to: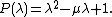
The coefficients are:
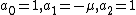
The associated Sturm series
Sturm series
In mathematics, the Sturm series associated with a pair of polynomials is named after Jacques Charles François Sturm.-Definition:Let p_0 and p_1 two univariate polynomials. Suppose that they do not have a common root and the degree of p_0 is greater than the degree of p_1...
is:
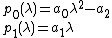
The Sturm
Sturm
Sturm may refer to:In persons:* Sturm , surname * Saint Sturm, 8th-century monkIn food:* Federweisser, known as Sturm in Austria, wine in the fermentation stage* Sturm Foods, an American dry grocery manufacturer...
polynomials can be written as (here
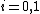 ):
):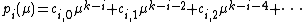
The above proposition 2 tells that one must have:
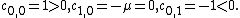
Because 1 > 0 and −1 < 0 are obvious, one can conclude that a Hopf bifurcation may occur for Van der Pol oscillator if
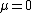 .
.External links
- Reaction-diffusion systems
- The Hopf Bifurcation
- Andronov–Hopf bifurcation page at ScholarpediaScholarpediaScholarpedia is an English-language online wiki-based encyclopedia that uses the same MediaWiki software as Wikipedia, but has features more commonly associated with open-access online academic journals....