Jacobian
Encyclopedia
In vector calculus, the Jacobian matrix (icon, rarely j) is the matrix
of all first-order partial derivative
s of a vector
- or scalar-valued function
with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space
to Euclidean m-space. Such a function is given by m real-valued component functions, y1(x1,...,xn), ..., ym(x1,...,xn). The partial derivatives of all these functions (if they exist) can be organized in an m-by-n matrix, the Jacobian matrix J of F, as follows:
This matrix is also denoted by
and 
. If (x1,...,xn) are the usual orthogonal Cartesian coordinates, the i th row (i = 1, ..., n) of this matrix corresponds to the gradient
of the ith component function yi: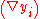
. Note that some books define the Jacobian as the transpose of the matrix given above.
The Jacobian determinant (often simply called the Jacobian) is the determinant
of the Jacobian matrix (if
).
These concepts are named after the mathematician
Carl Gustav Jacob Jacobi.
of a tangent plane to the function at a given point. In this way, the Jacobian generalizes the gradient
of a scalar valued function of multiple variables which itself generalizes the derivative of a scalar-valued function of a scalar. Likewise, the Jacobian can also be thought of as describing the amount of "stretching" that a transformation imposes. For example, if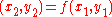
is used to transform an image, the Jacobian of f, 
describes how much the image in the neighborhood of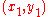 
is stretched in the x and y directions.
If a function is differentiable at a point, its derivative is given in coordinates by the Jacobian, but a function doesn't need to be differentiable for the Jacobian to be defined, since only the partial derivative
s are required to exist.
The importance of the Jacobian lies in the fact that it represents the best linear approximation to a differentiable function near a given point. In this sense, the Jacobian is the derivative of a multivariate function.
If p is a point in Rn and F is differentiable
at p, then its derivative is given by JF(p). In this case, the linear map described by JF(p) is the best linear approximation
of F near the point p, in the sense that
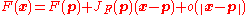
for x close to p and where o is the little o-notation (for
) and 
is the distance
between x and p.
In a sense, both the gradient
and Jacobian are "first derivatives
" the former the first derivative of a scalar function of several variables, the latter the first derivative of a vector function of several variables. In general, the gradient
can be regarded as a special version of the Jacobian: it is the Jacobian of a scalar function of several variables.
The Jacobian of the gradient
has a special name: the Hessian matrix
, which in a sense is the "second derivative
" of the scalar function of several variables in question.
, the matrix inverse of the Jacobian matrix of an invertible function is the Jacobian matrix of the inverse function. That is, for some function F : Rn → Rn and a point p in Rn,
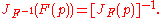
It follows that the (scalar) inverse of the Jacobian determinant of a transformation is the Jacobian determinant of the inverse transformation.
of the form x' = F(x), where x' is the (component-wise) time derivative of x, and F : Rn → Rn is continuous and differentiable. If F(x0) = 0, then x0 is a stationary point (also called a fixed point). The behavior of the system near a stationary point is related to the eigenvalues of JF(x0), the Jacobian of F at the stationary point. Specifically, if the eigenvalues all have a negative real part, then the system is stable in the operating point, if any eigenvalue has a positive real part, then the point is unstable.
, known as the Jacobian determinant. The Jacobian determinant is sometimes simply called "the Jacobian."
The Jacobian determinant at a given point gives important information about the behavior of F near that point. For instance, the continuously differentiable function F is invertible near a point p ∈ Rn if the Jacobian determinant at p is non-zero. This is the inverse function theorem
. Furthermore, if the Jacobian determinant at p is positive, then F preserves orientation near p; if it is negative, F reverses orientation. The absolute value
of the Jacobian determinant at p gives us the factor by which the function F expands or shrinks volume
s near p; this is why it occurs in the general substitution rule.
of a function over a region within its domain. To accommodate for the change of coordinates the magnitude of the Jacobian determinant arises as a multiplicative factor within the integral. Normally it is required that the change of coordinates be done in a manner which maintains an injectivity between the coordinates that determine the domain. The Jacobian determinant, as a result, is usually well defined.
(r, θ, φ) to Cartesian coordinates
(x1, x2, x3) , is given by the function F : R+ × [0,π] × [0,2π) → R3 with components:
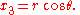
The Jacobian matrix for this coordinate change is
The determinant
is r2 sin θ. As an example, since dV = dx1 dx2 dx3 this determinant implies that the differential volume element dV = r2 sin θ dr dθ dϕ. Nevertheless this determinant varies with coordinates. To avoid any variation the new coordinates can be defined as
Now the determinant equals to 1 and volume element becomes 
.
Example 2. The Jacobian matrix of the function F : R3 → R4 with components
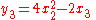
is
This example shows that the Jacobian need not be a square matrix.
Example 3.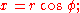
The Jacobian determinant is equal to
.
This shows how an integral in the Cartesian coordinate system
is transformed into an integral in the polar coordinate system
:
.
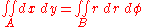Example 4.
The Jacobian determinant of the function F : R3 → R3 with components
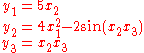
is
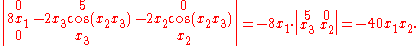
From this we see that F reverses orientation near those points where x1 and x2 have the same sign; the function is locally invertible everywhere except near points where x1 = 0 or x2 = 0. Intuitively, if you start with a tiny object around the point (1,1,1) and apply F to that object, you will get an object set with approximately 40 times the volume of the original one.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of all first-order partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of a vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
- or scalar-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
to Euclidean m-space. Such a function is given by m real-valued component functions, y1(x1,...,xn), ..., ym(x1,...,xn). The partial derivatives of all these functions (if they exist) can be organized in an m-by-n matrix, the Jacobian matrix J of F, as follows:
This matrix is also denoted by
and . If (x1,...,xn) are the usual orthogonal Cartesian coordinates, the i th row (i = 1, ..., n) of this matrix corresponds to the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the ith component function yi:
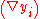. Note that some books define the Jacobian as the transpose of the matrix given above.The Jacobian determinant (often simply called the Jacobian) is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Jacobian matrix (if
).These concepts are named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Carl Gustav Jacob Jacobi.
Jacobian matrix
The Jacobian of a function describes the orientationOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of a tangent plane to the function at a given point. In this way, the Jacobian generalizes the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar valued function of multiple variables which itself generalizes the derivative of a scalar-valued function of a scalar. Likewise, the Jacobian can also be thought of as describing the amount of "stretching" that a transformation imposes. For example, if
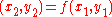is used to transform an image, the Jacobian of f, describes how much the image in the neighborhood of 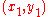is stretched in the x and y directions.If a function is differentiable at a point, its derivative is given in coordinates by the Jacobian, but a function doesn't need to be differentiable for the Jacobian to be defined, since only the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s are required to exist.
The importance of the Jacobian lies in the fact that it represents the best linear approximation to a differentiable function near a given point. In this sense, the Jacobian is the derivative of a multivariate function.
If p is a point in Rn and F is differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
at p, then its derivative is given by JF(p). In this case, the linear map described by JF(p) is the best linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
of F near the point p, in the sense that
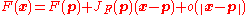
for x close to p and where o is the little o-notation (for
) and is the distanceEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between x and p.
In a sense, both the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and Jacobian are "first derivatives
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
" the former the first derivative of a scalar function of several variables, the latter the first derivative of a vector function of several variables. In general, the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
can be regarded as a special version of the Jacobian: it is the Jacobian of a scalar function of several variables.
The Jacobian of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
has a special name: the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
, which in a sense is the "second derivative
Second derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
" of the scalar function of several variables in question.
Inverse
According to the inverse function theoremInverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
, the matrix inverse of the Jacobian matrix of an invertible function is the Jacobian matrix of the inverse function. That is, for some function F : Rn → Rn and a point p in Rn,
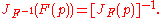
It follows that the (scalar) inverse of the Jacobian determinant of a transformation is the Jacobian determinant of the inverse transformation.
Dynamical systems
Consider a dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
of the form x
Newton's method
A system of coupled nonlinear equations can be solved iteratively by Newton's method. This method uses the Jacobian matrix of the system of equations.Jacobian determinant
If m = n, then F is a function from m-space to n-space and the Jacobian matrix is a square matrix. We can then form its determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
, known as the Jacobian determinant. The Jacobian determinant is sometimes simply called "the Jacobian."
The Jacobian determinant at a given point gives important information about the behavior of F near that point. For instance, the continuously differentiable function F is invertible near a point p ∈ Rn if the Jacobian determinant at p is non-zero. This is the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
. Furthermore, if the Jacobian determinant at p is positive, then F preserves orientation near p; if it is negative, F reverses orientation. The absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the Jacobian determinant at p gives us the factor by which the function F expands or shrinks volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
s near p; this is why it occurs in the general substitution rule.
Uses
The Jacobian determinant is used when making a change of variables when evaluating a multiple integralMultiple integral
The multiple integral is a type of definite integral extended to functions of more than one real variable, for example, ƒ or ƒ...
of a function over a region within its domain. To accommodate for the change of coordinates the magnitude of the Jacobian determinant arises as a multiplicative factor within the integral. Normally it is required that the change of coordinates be done in a manner which maintains an injectivity between the coordinates that determine the domain. The Jacobian determinant, as a result, is usually well defined.
Examples
Example 1. The transformation from spherical coordinatesSpherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
(r, θ, φ) to Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
(x1, x2, x3) , is given by the function F : R+ × [0,π] × [0,2π) → R3 with components:
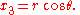
The Jacobian matrix for this coordinate change is
The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is r2 sin θ. As an example, since dV = dx1 dx2 dx3 this determinant implies that the differential volume element dV = r2 sin θ dr dθ dϕ. Nevertheless this determinant varies with coordinates. To avoid any variation the new coordinates can be defined as
Now the determinant equals to 1 and volume element becomes .Example 2. The Jacobian matrix of the function F : R3 → R4 with components
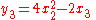
is
This example shows that the Jacobian need not be a square matrix.
Example 3.
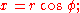
The Jacobian determinant is equal to
.This shows how an integral in the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is transformed into an integral in the polar coordinate system
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
:
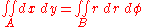.Example 4.
The Jacobian determinant of the function F : R3 → R3 with components
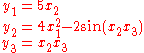
is
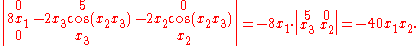
From this we see that F reverses orientation near those points where x1 and x2 have the same sign; the function is locally invertible everywhere except near points where x1 = 0 or x2 = 0. Intuitively, if you start with a tiny object around the point (1,1,1) and apply F to that object, you will get an object set with approximately 40 times the volume of the original one.
External links
- Mathworld A more technical explanation of Jacobians