
Branching process
Encyclopedia
In probability theory
, a branching process is a Markov process
that models a population in which each individual in generation n produces some random number of individuals in generation n + 1, according to a fixed probability distribution
that does not vary from individual to individual. Branching processes are used to model reproduction; for example, the individuals might correspond to bacteria, each of which generates 0, 1, or 2 offspring with some probability in a single time unit. Branching processes can also be used to model other systems with similar dynamics, e.g., the spread of surname
s in genealogy
or the propagation of neutrons in a nuclear reactor
.
A central question in the theory of branching processes is the probability of ultimate extinction, where no individuals exist after some finite number of generations. It is not hard to show that, starting with one individual in generation zero, the expected
size of generation n equals μ n where μ is the expected number of children of each individual. If μ is less than 1, then the expected number of individuals goes rapidly to zero, which implies ultimate extinction with probability 1 by Markov's inequality
. Alternatively, if μ is greater than 1, then the probability of ultimate extinction is less than 1 (but not necessarily zero; consider a process where each individual either dies without issue or has 100 children with equal probability). If μ is equal to 1, then ultimate extinction occurs with probability 1 unless each individual always has exactly one child.
In theoretical ecology
, the parameter μ of a branching process is called the basic reproductive rate.
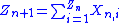
with Z0 = 1. Alternatively, one can formulate a branching process as a random walk
. Let Si denote the state in period i, and let Xi be a random variable that is iid over all i. Then the recurrence equation is
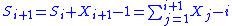
with S0 = 1. To gain some intuition for this formulation, one can imagine a walk where the goal is to visit every node, but every time a previously unvisited node is visited, additional nodes are revealed that must also be visited. Let Si represent the number of revealed but unvisited nodes in period i, and let Xi represent the number of new nodes that are revealed when node i is visited. Then in each period, the number of revealed but unvisited nodes equals the number of such nodes in the previous period, plus the new nodes that are revealed when visiting a node, minus the node that is visited. The process ends once all revealed nodes have been visited.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a branching process is a Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
that models a population in which each individual in generation n produces some random number of individuals in generation n + 1, according to a fixed probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
that does not vary from individual to individual. Branching processes are used to model reproduction; for example, the individuals might correspond to bacteria, each of which generates 0, 1, or 2 offspring with some probability in a single time unit. Branching processes can also be used to model other systems with similar dynamics, e.g., the spread of surname
Surname
A surname is a name added to a given name and is part of a personal name. In many cases, a surname is a family name. Many dictionaries define "surname" as a synonym of "family name"...
s in genealogy
Genealogy
Genealogy is the study of families and the tracing of their lineages and history. Genealogists use oral traditions, historical records, genetic analysis, and other records to obtain information about a family and to demonstrate kinship and pedigrees of its members...
or the propagation of neutrons in a nuclear reactor
Nuclear reactor
A nuclear reactor is a device to initiate and control a sustained nuclear chain reaction. Most commonly they are used for generating electricity and for the propulsion of ships. Usually heat from nuclear fission is passed to a working fluid , which runs through turbines that power either ship's...
.
A central question in the theory of branching processes is the probability of ultimate extinction, where no individuals exist after some finite number of generations. It is not hard to show that, starting with one individual in generation zero, the expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
size of generation n equals μ n where μ is the expected number of children of each individual. If μ is less than 1, then the expected number of individuals goes rapidly to zero, which implies ultimate extinction with probability 1 by Markov's inequality
Markov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
. Alternatively, if μ is greater than 1, then the probability of ultimate extinction is less than 1 (but not necessarily zero; consider a process where each individual either dies without issue or has 100 children with equal probability). If μ is equal to 1, then ultimate extinction occurs with probability 1 unless each individual always has exactly one child.
In theoretical ecology
Theoretical ecology
Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis...
, the parameter μ of a branching process is called the basic reproductive rate.
Mathematical formulation
The most common formulation of a branching process is that of the Galton–Watson process. Let Zn denote the state in period n (often interpreted as the size of generation n), and let Xn,i be a random variable denoting the number of direct successors of member i in period n, where Xn,i are iid over all n ∈ {0,1,2,...} and i ∈ {1,...,Zn}. Then the recurrence equation is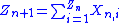
with Z0 = 1. Alternatively, one can formulate a branching process as a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
. Let Si denote the state in period i, and let Xi be a random variable that is iid over all i. Then the recurrence equation is
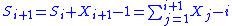
with S0 = 1. To gain some intuition for this formulation, one can imagine a walk where the goal is to visit every node, but every time a previously unvisited node is visited, additional nodes are revealed that must also be visited. Let Si represent the number of revealed but unvisited nodes in period i, and let Xi represent the number of new nodes that are revealed when node i is visited. Then in each period, the number of revealed but unvisited nodes equals the number of such nodes in the previous period, plus the new nodes that are revealed when visiting a node, minus the node that is visited. The process ends once all revealed nodes have been visited.
See also
- Galton–Watson process
- Random treeRandom treeIn mathematics and computer science, a random tree is a tree or arborescence that is formed by a stochastic process. Types of random trees include:...
- Branching random walkBranching random walkIn probability theory, a branching random walk is a stochastic process that generalizes both the concept of random walk and of branching process. At every generation , a branching random walk's value is a set of elements that are located in some linear space, such as the real line...
- MartingaleMartingaleMartingale can refer to:*Martingale , a stochastic process in which the conditional expectation of the next value, given the current and preceding values, is the current value*Martingale for horses...

