
Branching quantifier
Encyclopedia
In logic
a branching quantifier, also called a Henkin quantifier, finite partially ordered quantifier or even nonlinear quantifier, is a partial ordering

of quantifiers for Q∈{∀,∃}. It is a special case of generalized quantifier
. In classical logic
, quantifier prefixes are linearly ordered such that the value of a variable ym bound by a quantifier Qm depends on the value of the variables
bound by quantifiers
preceding Qm. In a logic with (finite) partially ordered quantification this is not in general the case.
Branching quantification first appeared in Leon Henkin
's "Some Remarks on Infinitely Long Formulas", Infinitistic Methods, Proceedings of the Symposium on Foundations of Mathematics, Warsaw, 1959. Systems of partially ordered quantification are intermediate in strength between first-order logic and second-order logic. They are being used as a basis for Hintikka's
and Gabriel Sandu's independence-friendly logic
(also known as informational-independence logic) which are claimed to be the most natural logics as a foundations for mathematics (e.g. set theory) or for capturing certain features of natural language and epistemology.
 is
is
 .
.
It (in fact every formula with a Henkin prefix, not just the simplest one) is equivalent to its second-order Skolemization, i.e.
 .
.
It is also powerful enough to define the quantifier (i.e. "there are infinitely many") defined as
(i.e. "there are infinitely many") defined as
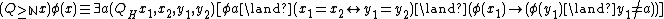 .
.
Several things follow from this, including the nonaxiomatizability of first-order logic with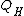 and its equivalence to the
and its equivalence to the 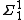 -fragment of second-order logic
-fragment of second-order logic
.
The following quantifiers are also definable by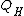 .
.
Rescher: "The number of φs is less than or equal to the number of ψs"

Härtig: "The φs are equinumerous with the ψs"
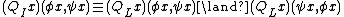
Chang: "The number of φs is equinumerous with the domain of the model"
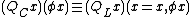
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
a branching quantifier, also called a Henkin quantifier, finite partially ordered quantifier or even nonlinear quantifier, is a partial ordering

of quantifiers for Q∈{∀,∃}. It is a special case of generalized quantifier
Generalized quantifier
In linguistic semantics, a generalized quantifier is an expression that denotes a property of a property, also called a higher-order property. This is the standard semantics assigned to quantified noun phrases, also called determiner phrases, in short: DP...
. In classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, quantifier prefixes are linearly ordered such that the value of a variable ym bound by a quantifier Qm depends on the value of the variables
- y1,...,ym-1
bound by quantifiers
- Qy1,...,Qym-1
preceding Qm. In a logic with (finite) partially ordered quantification this is not in general the case.
Branching quantification first appeared in Leon Henkin
Leon Henkin
Leon Albert Henkin was a logician at the University of California, Berkeley. He was principally known for the "Henkin's completeness proof": his version of the proof of the semantic completeness of standard systems of first-order logic.-The completeness proof:Henkin's result was not novel; it had...
's "Some Remarks on Infinitely Long Formulas", Infinitistic Methods, Proceedings of the Symposium on Foundations of Mathematics, Warsaw, 1959. Systems of partially ordered quantification are intermediate in strength between first-order logic and second-order logic. They are being used as a basis for Hintikka's
Jaakko Hintikka
Kaarlo Jaakko Juhani Hintikka is a Finnish philosopher and logician.Hintikka was born in Vantaa. After teaching for a number of years at Florida State University, Stanford, University of Helsinki, and the Academy of Finland, he is currently Professor of Philosophy at Boston University...
and Gabriel Sandu's independence-friendly logic
Independence-friendly logic
Independence-friendly logic , proposed by Jaakko Hintikka and Gabriel Sandu, aims at being a more natural and intuitive alternative to classical first-order logic . IF logic is characterized by branching quantifiers...
(also known as informational-independence logic) which are claimed to be the most natural logics as a foundations for mathematics (e.g. set theory) or for capturing certain features of natural language and epistemology.
Definable Quantifiers
The simplest Henkin quantifier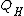 is
is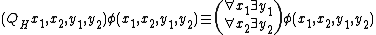 .
.It (in fact every formula with a Henkin prefix, not just the simplest one) is equivalent to its second-order Skolemization, i.e.
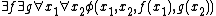 .
.It is also powerful enough to define the quantifier
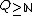 (i.e. "there are infinitely many") defined as
(i.e. "there are infinitely many") defined as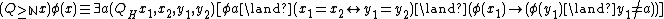 .
.Several things follow from this, including the nonaxiomatizability of first-order logic with
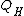 and its equivalence to the
and its equivalence to the 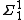 -fragment of second-order logic
-fragment of second-order logicSecond-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
.
The following quantifiers are also definable by
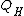 .
.Rescher: "The number of φs is less than or equal to the number of ψs"

Härtig: "The φs are equinumerous with the ψs"
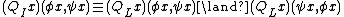
Chang: "The number of φs is equinumerous with the domain of the model"
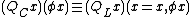
See also
- Game SemanticsGame semanticsGame semantics is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes. In the late 1950s Paul Lorenzen was the...
- Dependence Logic
- IF logicIndependence-friendly logicIndependence-friendly logic , proposed by Jaakko Hintikka and Gabriel Sandu, aims at being a more natural and intuitive alternative to classical first-order logic . IF logic is characterized by branching quantifiers...
- Mostowksi quantifier
- Lindström quantifierLindström quantifierIn mathematical logic, a Lindström quantifier is a generalized polyadic quantifier. They are a generalization of first-order quantifiers, such as the existential quantifier, the universal quantifier, and the counting quantifiers.They were introduced by Per Lindström in 1966.-Generalization of...
External links
- Game-theoretical quantifier at PlanetMath.

