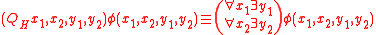Dependence logic
Encyclopedia
Dependence logic is a logical formalism, created by Jouko Väänänen, which adds dependence atoms to the language of first-order logic. A dependence atom is an expression of the form  , where
, where  are terms, and corresponds to the statement that the value of
are terms, and corresponds to the statement that the value of 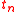 is functionally dependent
is functionally dependent
on the values of .
.
Dependence logic is a logic of imperfect information, like branching quantifier logic
or independence-friendly logic
: in other words, its game theoretic semantics
can be obtained from that of first-order logic by restricting the availability of information to the players, thus allowing for non-linearly ordered patterns of dependence and independence between variables. However, dependence logic differs from these logics in that it separates the notions of dependence and independence from the notion of quantification.
σ = (Sfunc, Srel, ar), the set of all well-formed dependence logic formulas is defined according to the following rules:
Nothing else is an atomic formula of dependence logic.
Relational and equality atoms are also called first order atoms.
 of dependence logic and their respective sets of free variables
of dependence logic and their respective sets of free variables  are defined as follows:
are defined as follows:
Nothing is a dependence logic formula unless it can be obtained through a finite number of applications of these four rules.
A formula such that
such that  is a sentence of dependence logic.
is a sentence of dependence logic.
Therefore, is taken as a shorthand for
is taken as a shorthand for 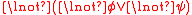 , and
, and 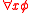 is taken as a shorthand for
is taken as a shorthand for 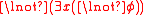 .
.
' compositional semantics for IF logic
. There exist equivalent game-theoretic semantics for dependence logic, both in terms of imperfect information games and in terms of perfect information games.
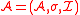 be a first-order structure
be a first-order structure
and let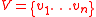 be a finite set of variables. Then a team over
be a finite set of variables. Then a team over  with domain
with domain 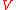 is a set of assignments over
is a set of assignments over  with domain
with domain 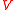 , that is, a set of functions
, that is, a set of functions  from
from  to
to  .
.
It may be helpful to visualize such a team as a database relation
with attributes and with only one data type, corresponding to the domain
and with only one data type, corresponding to the domain  of the structure: for example, if the team
of the structure: for example, if the team  consists of four assignments
consists of four assignments  with domain
with domain 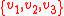 then one may represent it as the relation
then one may represent it as the relation
 and
and  between structures, teams and formulas.
between structures, teams and formulas.
Given a structure , a team
, a team  over it and a dependence logic formula
over it and a dependence logic formula  whose free variables
whose free variables
are contained in the domain of , if
, if 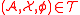 we say that
we say that  is a trump for
is a trump for  in
in  , and we write that
, and we write that  ; and analogously, if
; and analogously, if  we say that
we say that  is a cotrump for
is a cotrump for  in
in  , and we write that
, and we write that  .
.
If one can also say that
one can also say that  is positively satisfied by
is positively satisfied by  in
in  , and if instead
, and if instead  one can say that
one can say that  is negatively satisfied by
is negatively satisfied by  in
in  .
.
The necessity of considering positive and negative satisfaction separately is a consequence of the fact that in dependence logic, as in the logic of branching quantifiers
or in IF logic
, the law of the excluded middle does not hold; alternatively, one may assume that all formulas are in negation normal form, using De Morgan's relations in order to define universal quantification and conjunction from existential quantification and disjunction respectively, and consider positive satisfaction alone.
Given a sentence , we say that
, we say that  is true in
is true in  if and only if
if and only if  , and we say that
, and we say that  is false in
is false in  if and only if
if and only if  .
.
's satisfiability relation for first-order formulas, the positive and negative satisfiability relations of the team semantics for dependence logic are defined by structural induction
over the formulas of the language. Since the negation operator interchanges positive and negative satisfiability, the two inductions corresponding to and
and  need to be performed simultaneously:
need to be performed simultaneously:
of first-order logic: in other words, for every first order sentence and structure
and structure  we have that
we have that  if and only if
if and only if  is true in
is true in  according to the usual first order semantics. Furthemore, for any first order formula
according to the usual first order semantics. Furthemore, for any first order formula  ,
,  if and only if all assignments
if and only if all assignments 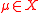 satisfy
satisfy  in
in  according to the usual first order semantics.
according to the usual first order semantics.
However, dependence logic is strictly more expressive than first order logic: for example, the sentence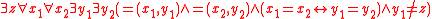
is true in a model if and only if the domain of this model is infinite, even though no first order formula
if and only if the domain of this model is infinite, even though no first order formula  has this property.
has this property.

where does not contain second order quantifiers.
does not contain second order quantifiers.
Conversely, every second-order sentence in the above form is equivalent to some dependence logic sentence.
As for open formulas, dependence logic corresponds to the downwards monotone fragment of existential second order logic, in the sense that a nonempty class of teams is definable by a dependence logic formula if and only if the corresponding class of relations is downwards monotone and definable by an existential second order formula.
is equivalent to the dependence logic sentence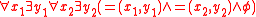 , in the sense that the former expression is true in a model if and only if the latter expression is true.
, in the sense that the former expression is true in a model if and only if the latter expression is true.
Conversely, any dependence logic sentence is equivalent to some sentence in the logic of branching quantifiers, since all existential second order sentences are expressible in branching quantifier logic.
However, the issue is subtler when it comes to open formulas. Translations between IF logic and dependence logic formulas, and vice versa, exist as long as the domain of the team is fixed: in other words, for all sets of variables and all IF logic formulas
and all IF logic formulas  with free variables in
with free variables in 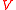 there exists a dependence logic formula
there exists a dependence logic formula 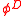 such that
such that
for all structures and for all teams
and for all teams  with domain
with domain 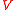 , and conversely, for every dependence logic formula
, and conversely, for every dependence logic formula 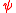 with free variables in
with free variables in 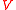 there exists an IF logic formula
there exists an IF logic formula 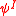 such that
such that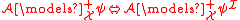
for all structures and for all teams
and for all teams  with domain
with domain 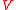 . These translations cannot be compositional.
. These translations cannot be compositional.
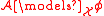 and
and  then
then 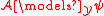 . Furthermore, the empty team (but not the team containing the empty assignment) satisfies all formulas of Dependence Logic, both positively and negatively.
. Furthermore, the empty team (but not the team containing the empty assignment) satisfies all formulas of Dependence Logic, both positively and negatively.
The law of the excluded middle fails in dependence logic: for example, the formula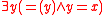 is neither positively nor negatively satisfied by the team
is neither positively nor negatively satisfied by the team  . Furthermore, disjunction is not idempotent and does not distribute over conjunction.
. Furthermore, disjunction is not idempotent and does not distribute over conjunction.
Both the compactness theorem
and the Löwenheim-Skolem theorem are true for dependence logic. Craig's interpolation theorem
also holds, but, due to the nature of negation in dependence logic, in a slightly modified formulation: if two dependence logic formulas and
and 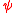 are contradictory, that is, it is never the case that both
are contradictory, that is, it is never the case that both  and
and 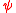 hold in the same model, then there exists a first order sentence
hold in the same model, then there exists a first order sentence  in the common language of the two sentences such that
in the common language of the two sentences such that  implies
implies  and
and  is contradictory with
is contradictory with 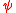 .
.
As IF logic, Dependence logic can define its own truth operator: more precisely, there exists a formula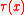 such that for every sentence
such that for every sentence  of dependence logic and all models
of dependence logic and all models 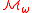 which satisfy Peano's axioms, if
which satisfy Peano's axioms, if 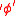 is the Gödel number of
is the Gödel number of  then
then
This does not contradict Tarski's undefinability theorem, since the negation of dependence logic is not the usual contradictory one.
, the model checking problem for dependence logic is NP-complete
. Furthermore, its inconsistency problem is semidecidable, and in fact equivalent to the inconsistency problem for first-order logic.
However, the decision problem for dependence logic is non-arithmetical
, and is in fact complete with respect to the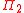 class of the Levy hierarchy.
class of the Levy hierarchy.
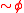 . Its expressive power is equivalent to that of full second order logic.
. Its expressive power is equivalent to that of full second order logic.
, thus obtaining modal dependence logic.
 , whose name derives from the similarity between its definition and that of the implication of intuitionistic logic
, whose name derives from the similarity between its definition and that of the implication of intuitionistic logic
, can be defined as follows:
Intuitionistic dependence logic, that is, dependence logic supplemented with the intuitionistic implication, is equivalent to second-order logic.
 , where
, where  are terms, and corresponds to the statement that the value of
are terms, and corresponds to the statement that the value of 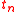 is functionally dependent
is functionally dependentFunctional dependency
A functional dependency is a constraint between two sets of attributes in a relation from a database.Given a relation R, a set of attributes X in R is said to functionally determine another attribute Y, also in R, if, and only if, each X value is associated with precisely one Y value...
on the values of
 .
.Dependence logic is a logic of imperfect information, like branching quantifier logic
Branching quantifier
In logic a branching quantifier, also called a Henkin quantifier, finite partially ordered quantifier or even nonlinear quantifier, is a partial ordering\langle Qx_1\dots Qx_n\rangle...
or independence-friendly logic
Independence-friendly logic
Independence-friendly logic , proposed by Jaakko Hintikka and Gabriel Sandu, aims at being a more natural and intuitive alternative to classical first-order logic . IF logic is characterized by branching quantifiers...
: in other words, its game theoretic semantics
Game semantics
Game semantics is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes. In the late 1950s Paul Lorenzen was the...
can be obtained from that of first-order logic by restricting the availability of information to the players, thus allowing for non-linearly ordered patterns of dependence and independence between variables. However, dependence logic differs from these logics in that it separates the notions of dependence and independence from the notion of quantification.
Syntax
The syntax of dependence logic is an extension of that of first-order logic. For a fixed signatureSignature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
σ = (Sfunc, Srel, ar), the set of all well-formed dependence logic formulas is defined according to the following rules:
Terms
Terms in dependence logic are defined precisely as in first-order logic.Atomic formulas
There are three types of atomic formulas in dependence logic:- A relational atom is an expression of the form
 for any n-ary relation
for any n-ary relation  in our signature and for any n-uple of terms
in our signature and for any n-uple of terms  ;
; - An equality atom is an expression of the form
 , for any two terms
, for any two terms 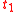 and
and 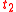 ;
; - A dependence atom is an expression of the form
 , for any
, for any  and for any n-uple of terms
and for any n-uple of terms  .
.
Nothing else is an atomic formula of dependence logic.
Relational and equality atoms are also called first order atoms.
Complex formulas and sentences
For a fixed signature σ, the set of all formulas of dependence logic and their respective sets of free variables
of dependence logic and their respective sets of free variables  are defined as follows:
are defined as follows:- Any atomic formula
 is a formula, and
is a formula, and  is the set of all variables occurring in it;
is the set of all variables occurring in it; - If
 is a formula, so is
is a formula, so is  and
and 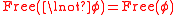 ;
; - If
 and
and 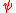 are formulas, so is
are formulas, so is 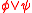 and
and  ;
; - If
 is a formula and
is a formula and  is a variable,
is a variable,  is also a formula and
is also a formula and 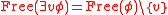 .
.
Nothing is a dependence logic formula unless it can be obtained through a finite number of applications of these four rules.
A formula
 such that
such that 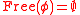 is a sentence of dependence logic.
is a sentence of dependence logic.Conjunction and universal quantification
In the above presentation of the syntax of dependence logic, conjunction and universal quantification are not treated as primitive operators; rather, they are defined in terms of disjunction and negation and existential quantification respectively, by means of De Morgan's Laws.Therefore,
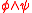 is taken as a shorthand for
is taken as a shorthand for 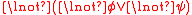 , and
, and 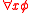 is taken as a shorthand for
is taken as a shorthand for 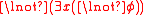 .
.Semantics
The team semantics for dependence logic is a variant of Wilfrid HodgesWilfrid Hodges
Wilfrid Augustine Hodges is a British mathematician, known for his work in model theory. He was Professor of Mathematics at Queen Mary, University of London from 1987 to 2006, and is the author of numerous books on logic....
' compositional semantics for IF logic
Independence-friendly logic
Independence-friendly logic , proposed by Jaakko Hintikka and Gabriel Sandu, aims at being a more natural and intuitive alternative to classical first-order logic . IF logic is characterized by branching quantifiers...
. There exist equivalent game-theoretic semantics for dependence logic, both in terms of imperfect information games and in terms of perfect information games.
Teams
Let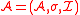 be a first-order structure
be a first-order structureStructure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
and let
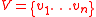 be a finite set of variables. Then a team over
be a finite set of variables. Then a team over  with domain
with domain 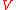 is a set of assignments over
is a set of assignments over  with domain
with domain 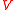 , that is, a set of functions
, that is, a set of functions  from
from  to
to  .
.It may be helpful to visualize such a team as a database relation
Relation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
with attributes
 and with only one data type, corresponding to the domain
and with only one data type, corresponding to the domain  of the structure: for example, if the team
of the structure: for example, if the team  consists of four assignments
consists of four assignments  with domain
with domain 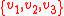 then one may represent it as the relation
then one may represent it as the relation
 |
 |
 |
|
|---|---|---|---|
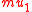 |
 |
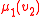 |
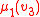 |
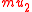 |
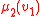 |
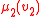 |
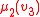 |
 |
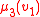 |
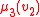 |
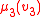 |
 |
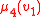 |
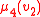 |
 |
Positive and negative satisfaction
Team semantics can be defined in terms of two relations and
and  between structures, teams and formulas.
between structures, teams and formulas.Given a structure
 , a team
, a team  over it and a dependence logic formula
over it and a dependence logic formula  whose free variables
whose free variablesFree variables and bound variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
are contained in the domain of
 , if
, if 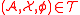 we say that
we say that  is a trump for
is a trump for  in
in  , and we write that
, and we write that  ; and analogously, if
; and analogously, if  we say that
we say that  is a cotrump for
is a cotrump for  in
in  , and we write that
, and we write that  .
.If
 one can also say that
one can also say that  is positively satisfied by
is positively satisfied by  in
in  , and if instead
, and if instead  one can say that
one can say that  is negatively satisfied by
is negatively satisfied by  in
in  .
.The necessity of considering positive and negative satisfaction separately is a consequence of the fact that in dependence logic, as in the logic of branching quantifiers
Branching quantifier
In logic a branching quantifier, also called a Henkin quantifier, finite partially ordered quantifier or even nonlinear quantifier, is a partial ordering\langle Qx_1\dots Qx_n\rangle...
or in IF logic
Independence-friendly logic
Independence-friendly logic , proposed by Jaakko Hintikka and Gabriel Sandu, aims at being a more natural and intuitive alternative to classical first-order logic . IF logic is characterized by branching quantifiers...
, the law of the excluded middle does not hold; alternatively, one may assume that all formulas are in negation normal form, using De Morgan's relations in order to define universal quantification and conjunction from existential quantification and disjunction respectively, and consider positive satisfaction alone.
Given a sentence
 , we say that
, we say that  is true in
is true in  if and only if
if and only if  , and we say that
, and we say that  is false in
is false in  if and only if
if and only if  .
.Semantic rules
As for the case of Alfred TarskiAlfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
's satisfiability relation for first-order formulas, the positive and negative satisfiability relations of the team semantics for dependence logic are defined by structural induction
Structural induction
Structural induction is a proof method that is used in mathematical logic , computer science, graph theory, and some other mathematical fields. It is a generalization of mathematical induction...
over the formulas of the language. Since the negation operator interchanges positive and negative satisfiability, the two inductions corresponding to
 and
and  need to be performed simultaneously:
need to be performed simultaneously:Positive satisfiability
-
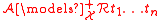 if and only if
if and only if
-
 is a n-ary symbol in the signature of
is a n-ary symbol in the signature of  ;
; - All variables occurring in the terms
 are in the domain of
are in the domain of  ;
; - For every assignment
 , the evaluation of the tuple
, the evaluation of the tuple  according to
according to  is in the interpretation of
is in the interpretation of  in
in  ;
;
-
-
 if and only if
if and only if
- All variables occurring in the terms
 and
and  are in the domain of
are in the domain of  ;
; - For every assignment
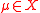 , the evaluations of
, the evaluations of 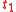 and
and 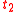 according to
according to  are the same;
are the same;
- All variables occurring in the terms
-
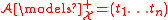 if and only if any two assignments
if and only if any two assignments 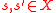 whose evaluations of the tuple
whose evaluations of the tuple  coincide assign the same value to
coincide assign the same value to 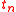 ;
; -
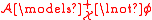 if and only if
if and only if  ;
; -
 if and only if there exist teams
if and only if there exist teams  and
and  such that
such that
-
 '
' -
 ;
; -
 ;
;
-
-
 if and only if there exists a function
if and only if there exists a function  from
from  to the domain of
to the domain of  such that
such that  , where
, where 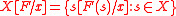 .
.
Negative satisfiability
-
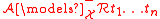 if and only if
if and only if
-
 is a n-ary symbol in the signature of
is a n-ary symbol in the signature of  ;
; - All variables occurring in the terms
 are in the domain of
are in the domain of  ;
; - For every assignment
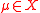 , the evaluation of the tuple
, the evaluation of the tuple  according to
according to  is not in the interpretation of
is not in the interpretation of  in
in  ;
;
-
-
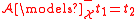 if and only if
if and only if
- All variables occurring in the terms
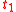 and
and 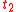 are in the domain of
are in the domain of  ;
; - For every assignment
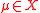 , the evaluations of
, the evaluations of 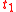 and
and  according to
according to  are different;
are different;
- All variables occurring in the terms
-
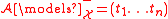 if and only if
if and only if  is the empty team;
is the empty team; -
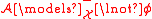 if and only if
if and only if  ;
; -
 if and only if
if and only if  and
and  ;
; -
 if and only if
if and only if 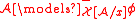 , where
, where 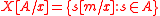 and
and  is the domain of
is the domain of  .
.
Dependence logic and first-order logic
Dependence logic is a conservative extensionConservative extension
In mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
of first-order logic: in other words, for every first order sentence
 and structure
and structure  we have that
we have that  if and only if
if and only if  is true in
is true in  according to the usual first order semantics. Furthemore, for any first order formula
according to the usual first order semantics. Furthemore, for any first order formula  ,
,  if and only if all assignments
if and only if all assignments 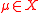 satisfy
satisfy  in
in  according to the usual first order semantics.
according to the usual first order semantics.However, dependence logic is strictly more expressive than first order logic: for example, the sentence
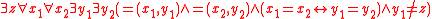
is true in a model
 if and only if the domain of this model is infinite, even though no first order formula
if and only if the domain of this model is infinite, even though no first order formula  has this property.
has this property.Dependence logic and second-order logic
Every dependence logic sentence is equivalent to some sentence in the existential fragment of second order logic, that is, to some second order sentence of the form
where
 does not contain second order quantifiers.
does not contain second order quantifiers.Conversely, every second-order sentence in the above form is equivalent to some dependence logic sentence.
As for open formulas, dependence logic corresponds to the downwards monotone fragment of existential second order logic, in the sense that a nonempty class of teams is definable by a dependence logic formula if and only if the corresponding class of relations is downwards monotone and definable by an existential second order formula.
Dependence logic and branching quantifiers
Branching quantifiers are expressible in terms of dependence atoms: for example, the expressionis equivalent to the dependence logic sentence
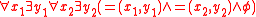 , in the sense that the former expression is true in a model if and only if the latter expression is true.
, in the sense that the former expression is true in a model if and only if the latter expression is true.Conversely, any dependence logic sentence is equivalent to some sentence in the logic of branching quantifiers, since all existential second order sentences are expressible in branching quantifier logic.
Dependence logic and IF logic
Any dependence logic sentence is logically equivalent to some IF logic sentence, and vice versa.However, the issue is subtler when it comes to open formulas. Translations between IF logic and dependence logic formulas, and vice versa, exist as long as the domain of the team is fixed: in other words, for all sets of variables
 and all IF logic formulas
and all IF logic formulas  with free variables in
with free variables in 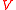 there exists a dependence logic formula
there exists a dependence logic formula 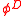 such that
such that
for all structures
 and for all teams
and for all teams  with domain
with domain 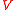 , and conversely, for every dependence logic formula
, and conversely, for every dependence logic formula 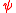 with free variables in
with free variables in 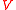 there exists an IF logic formula
there exists an IF logic formula 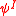 such that
such that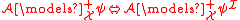
for all structures
 and for all teams
and for all teams  with domain
with domain 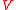 . These translations cannot be compositional.
. These translations cannot be compositional.Properties
Dependence logic formulas are downwards closed: if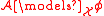 and
and  then
then 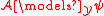 . Furthermore, the empty team (but not the team containing the empty assignment) satisfies all formulas of Dependence Logic, both positively and negatively.
. Furthermore, the empty team (but not the team containing the empty assignment) satisfies all formulas of Dependence Logic, both positively and negatively.The law of the excluded middle fails in dependence logic: for example, the formula
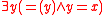 is neither positively nor negatively satisfied by the team
is neither positively nor negatively satisfied by the team  . Furthermore, disjunction is not idempotent and does not distribute over conjunction.
. Furthermore, disjunction is not idempotent and does not distribute over conjunction.Both the compactness theorem
Compactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
and the Löwenheim-Skolem theorem are true for dependence logic. Craig's interpolation theorem
Craig interpolation
In mathematical logic, Craig's interpolation theorem is a result about the relationship between different logical theories. Roughly stated, the theorem says that if a formula φ implies a formula ψ then there is a third formula ρ, called an interpolant, such that every nonlogical symbol...
also holds, but, due to the nature of negation in dependence logic, in a slightly modified formulation: if two dependence logic formulas
 and
and 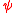 are contradictory, that is, it is never the case that both
are contradictory, that is, it is never the case that both  and
and 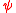 hold in the same model, then there exists a first order sentence
hold in the same model, then there exists a first order sentence  in the common language of the two sentences such that
in the common language of the two sentences such that  implies
implies  and
and  is contradictory with
is contradictory with 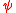 .
.As IF logic, Dependence logic can define its own truth operator: more precisely, there exists a formula
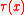 such that for every sentence
such that for every sentence  of dependence logic and all models
of dependence logic and all models 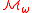 which satisfy Peano's axioms, if
which satisfy Peano's axioms, if 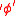 is the Gödel number of
is the Gödel number of  then
then
-
 if and only if
if and only if 
This does not contradict Tarski's undefinability theorem, since the negation of dependence logic is not the usual contradictory one.
Complexity
As a consequence of Fagin's theoremFagin's theorem
Fagin's theorem is a result in descriptive complexity theory that states that the set of all properties expressible in existential second-order logic is precisely the complexity class NP...
, the model checking problem for dependence logic is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. Furthermore, its inconsistency problem is semidecidable, and in fact equivalent to the inconsistency problem for first-order logic.
However, the decision problem for dependence logic is non-arithmetical
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
, and is in fact complete with respect to the
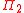 class of the Levy hierarchy.
class of the Levy hierarchy.Team logic
Team logic extends dependence logic with a contradictory negation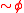 . Its expressive power is equivalent to that of full second order logic.
. Its expressive power is equivalent to that of full second order logic.Modal dependence logic
The dependence atom, or a suitable variant thereof, can be added to the language of modal logicModal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
, thus obtaining modal dependence logic.
Intuitionistic dependence logic
As it is, dependence logic lacks an implication. The intuitionistic implication , whose name derives from the similarity between its definition and that of the implication of intuitionistic logic
, whose name derives from the similarity between its definition and that of the implication of intuitionistic logicIntuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
, can be defined as follows:
-
 if and only if for all
if and only if for all  such that
such that 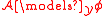 it holds that
it holds that 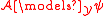 .
.
Intuitionistic dependence logic, that is, dependence logic supplemented with the intuitionistic implication, is equivalent to second-order logic.