Breather
Encyclopedia
A breather is a nonlinear wave
in which energy concentrates in a localized and oscillatory fashion. This contradicts with the expectations derived from the corresponding linear system for infinitesimal
amplitude
s, which tends towards an even distribution of initially localized energy.
A discrete breather is a breather solution on a nonlinear lattice
.
The term breather originates from the characteristic that most breathers are localized in space and oscillate (breathe) in time. But also the opposite situation: oscillations in space and localized in time, is denoted as a breather.
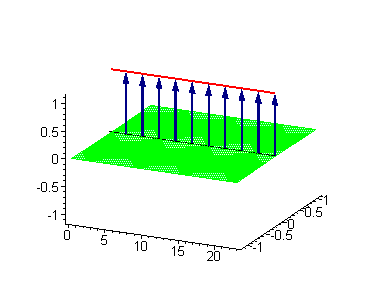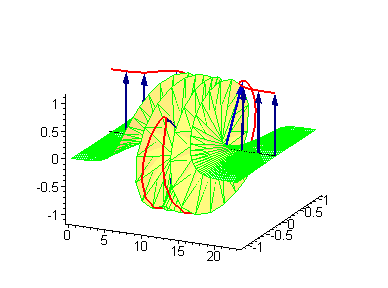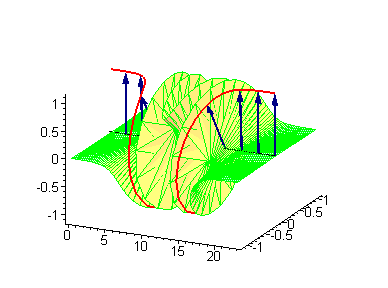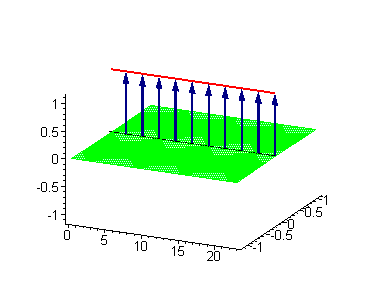
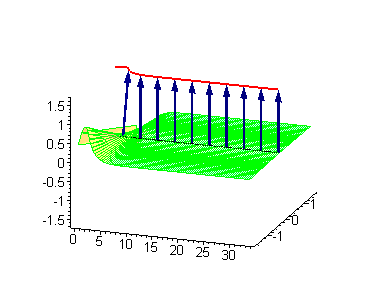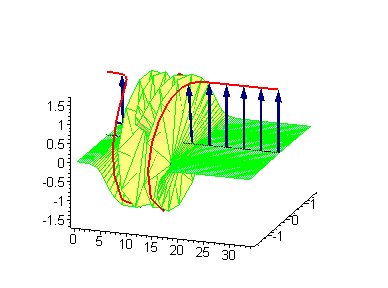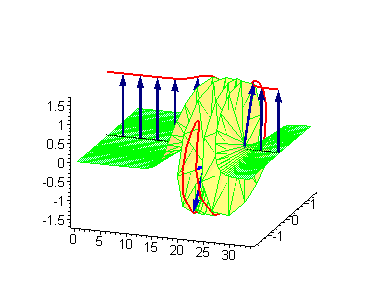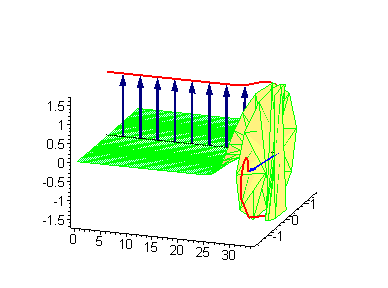A breather is a localized period
ic solution of either continuous media
equations or discrete lattice
equations. The exactly solvable sine-Gordon equation
and the focusing nonlinear Schrödinger equation
are examples of one-dimensional partial differential equation
s that possess breather solutions. Discrete nonlinear Hamiltonian lattices in many cases support breather solutions.
Breathers are soliton
ic structures. There are two types of breathers: standing
or traveling ones. Standing breathers correspond to localized solutions whose amplitude vary in time (they are sometimes called oscillon
s). A necessary condition for the existence of breathers in discrete lattices is that the breather main frequency
and all its multipliers are located outside of the phonon
spectrum
of the lattice.
is the nonlinear dispersive partial differential equation
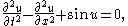
with the field
u a function of the spatial coordinate x and time t.
An exact solution found by using the inverse scattering transform
is:
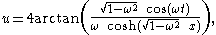
which, for ω < 1, is periodic in time t and decays exponentially when moving away from x = 0.
is the dispersive partial differential equation:
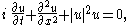
with u a complex
field as a function of x and t. Further i denotes the imaginary unit
.
One of the breather solutions is
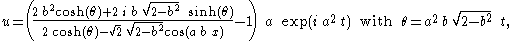
which gives breathers periodic in space x and approaching the uniform value a when moving away from the focus time t = 0. These breathers exist for values of the modulation
parameter b less than √ 2.
Note that a limiting case of the breather solution is the Peregrine soliton
.
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
in which energy concentrates in a localized and oscillatory fashion. This contradicts with the expectations derived from the corresponding linear system for infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
s, which tends towards an even distribution of initially localized energy.
A discrete breather is a breather solution on a nonlinear lattice
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
.
The term breather originates from the characteristic that most breathers are localized in space and oscillate (breathe) in time. But also the opposite situation: oscillations in space and localized in time, is denoted as a breather.
Overview
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
ic solution of either continuous media
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
equations or discrete lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
equations. The exactly solvable sine-Gordon equation
Sine-Gordon equation
The sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative...
and the focusing nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
are examples of one-dimensional partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s that possess breather solutions. Discrete nonlinear Hamiltonian lattices in many cases support breather solutions.
Breathers are soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
ic structures. There are two types of breathers: standing
Standing wave
In physics, a standing wave – also known as a stationary wave – is a wave that remains in a constant position.This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling...
or traveling ones. Standing breathers correspond to localized solutions whose amplitude vary in time (they are sometimes called oscillon
Oscillon
In physics, an oscillon is a soliton-like phenomenon that occurs in granular and other dissipative media. Oscillons in granular media result from vertically vibrating a plate with a layer of uniform particles placed freely on top...
s). A necessary condition for the existence of breathers in discrete lattices is that the breather main frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
and all its multipliers are located outside of the phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of the lattice.
Example of a breather solution for the sine-Gordon equation
The sine-Gordon equationSine-Gordon equation
The sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative...
is the nonlinear dispersive partial differential equation
Dispersive partial differential equation
In mathematics, a dispersive partial differential equation or dispersive PDE is a partial differential equation that is dispersive. In this context, dispersion means that waves of different wavelength propagate at different phase velocities....
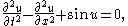
with the field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
u a function of the spatial coordinate x and time t.
An exact solution found by using the inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
is:
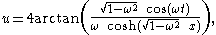
which, for ω < 1, is periodic in time t and decays exponentially when moving away from x = 0.
Example of a breather solution for the nonlinear Schrödinger equation
The focusing nonlinear Schrödinger equationNonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
is the dispersive partial differential equation:
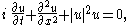
with u a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
field as a function of x and t. Further i denotes the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
One of the breather solutions is
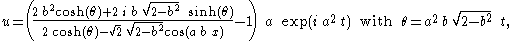
which gives breathers periodic in space x and approaching the uniform value a when moving away from the focus time t = 0. These breathers exist for values of the modulation
Modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a high-frequency periodic waveform, called the carrier signal, with a modulating signal which typically contains information to be transmitted...
parameter b less than √ 2.
Note that a limiting case of the breather solution is the Peregrine soliton
Peregrine soliton
The Peregrine soliton is an analytic solution of the nonlinear Schrödinger equation. This solution has been proposed in 1983 by Howell Peregrine, researcher at the mathematics department of the University of Bristol.- Main properties :...
.