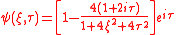Peregrine soliton
Encyclopedia
The Peregrine soliton is an analytic solution of the nonlinear Schrödinger equation
. This solution has been proposed in 1983 by Howell Peregrine
, researcher at the mathematics department of the University of Bristol
.
that can maintain its profile unchanged during propagation, the Peregrine soliton presents a double spatio-temporal localization. Therefore, starting from a weak oscillation on a continuous background, the Peregrine soliton develops undergoing a progressive increase of its amplitude and a narrowing of its temporal duration. At the point of maximum compression, the amplitude is three times the level of the continuous background (and if one considers the intensity as it is relevant in optics, there is a factor 9 between the peak intensity and the surrounding background). After this point of maximal compression, the wave's amplitude decreases and its width increases and it finally vanishes.
These features of the Peregrine soliton are fully consistent with the quantitative criteria usually used in order to qualify a wave as a rogue wave. Therefore, the Peregrine soliton is an attractive hypothesis to explain the formation of those waves which have a high amplitude and may appear from nowhere and disappear without a trace.
with the spatial coordinate and
the spatial coordinate and  the temporal coordinate.
the temporal coordinate. 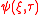 being the envelope
being the envelope
of a surface wave in deep water. The dispersion
is anomalous and the nonlinearity is self-focusing
(note that similar results could be obtained for a normally dispersive medium combined with a defocusing nonlinearity).
The Peregrine analytical expression is :
so that the temporal and spatial maxima are obtained for and
and  .
.
The Peregrine soliton is a first-order rational soliton. It can also be seen as a limiting case of an Akhmediev breather
.
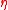 :
:

with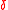 being the Dirac delta function
being the Dirac delta function
.
This corresponds to a modulus
(with the constant continuous background here omitted) :
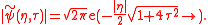
Quite interestingly, one can notice that for any given time , the modulus of the spectrum exhibits a typical triangular shape when plotted on a logarithmic scale. The broadest spectrum is obtained for
, the modulus of the spectrum exhibits a typical triangular shape when plotted on a logarithmic scale. The broadest spectrum is obtained for  , which corresponds to the maximum of compression of the spatio-temporal nonlinear structure.
, which corresponds to the maximum of compression of the spatio-temporal nonlinear structure.
In 2010, more than 25 years after the initial work of Peregrine, researchers took advantage of the analogy that can be drawn between hydrodynamics and optics in order to generate Peregrine solitons in optical fiber
s. In fact, the evolution of light in fiber optics and the evolution of surface waves in deep water are both modelled by the nonlinear Schrödinger equation (note however that spatial and temporal variables have to be switched). Such an analogy has been exploited in the past in order to generate optical solitons
in optical fibers. Interestingly, by using exclusively standard optical communication
components, it has been shown that even with an approximate initial condition (in the case of this work, an initial sinosoidal beating), a profile very close to the ideal Peregrine soliton can be generated. The typical triangular spectral shape has also been experimentally confirmed.
These results in optics have been confirmed in 2011 in hydrodynamics with experiments carried out in a 15-m long water wave tank. Other experiments carried out in the physics of plasmas
have also highlighted the emergence of Peregrine solitons in other fields ruled by the nonlinear Schrodinger equation .
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
. This solution has been proposed in 1983 by Howell Peregrine
Howell Peregrine
Howell Peregrine was a British applied mathematician noted for his contributions to fluid mechanics, especially of free surface flows such as water waves, and coastal engineering.- Education and career :...
, researcher at the mathematics department of the University of Bristol
University of Bristol
The University of Bristol is a public research university located in Bristol, United Kingdom. One of the so-called "red brick" universities, it received its Royal Charter in 1909, although its predecessor institution, University College, Bristol, had been in existence since 1876.The University is...
.
Main properties
Contrary to the usual fundamental solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
that can maintain its profile unchanged during propagation, the Peregrine soliton presents a double spatio-temporal localization. Therefore, starting from a weak oscillation on a continuous background, the Peregrine soliton develops undergoing a progressive increase of its amplitude and a narrowing of its temporal duration. At the point of maximum compression, the amplitude is three times the level of the continuous background (and if one considers the intensity as it is relevant in optics, there is a factor 9 between the peak intensity and the surrounding background). After this point of maximal compression, the wave's amplitude decreases and its width increases and it finally vanishes.
These features of the Peregrine soliton are fully consistent with the quantitative criteria usually used in order to qualify a wave as a rogue wave. Therefore, the Peregrine soliton is an attractive hypothesis to explain the formation of those waves which have a high amplitude and may appear from nowhere and disappear without a trace.
In the spatio-temporal domain
The Peregrine soliton is a solution of the one-dimensional nonlinear Schrödinger equation that can be written in normalized units as follows :with
 the spatial coordinate and
the spatial coordinate and  the temporal coordinate.
the temporal coordinate. 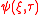 being the envelope
being the envelopeEnvelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of a surface wave in deep water. The dispersion
Dispersion
Dispersion may refer to:In physics:*The dependence of wave velocity on frequency or wavelength:**Dispersion , for light waves**Dispersion **Acoustic dispersion, for sound waves...
is anomalous and the nonlinearity is self-focusing
Self-focusing
Self-focusing is a non-linear optical process induced by the change in refractive index of materials exposed to intense electromagnetic radiation. A medium whose refractive index increases with the electric field intensity acts as a focusing lens for an electromagnetic wave characterised by an...
(note that similar results could be obtained for a normally dispersive medium combined with a defocusing nonlinearity).
The Peregrine analytical expression is :
so that the temporal and spatial maxima are obtained for
 and
and  .
.The Peregrine soliton is a first-order rational soliton. It can also be seen as a limiting case of an Akhmediev breather
Breather
A breather is a nonlinear wave in which energy concentrates in a localized and oscillatory fashion. This contradicts with the expectations derived from the corresponding linear system for infinitesimal amplitudes, which tends towards an even distribution of initially localized energy.A discrete...
.
In the spectral domain
It is also possible to mathematically express the Peregrine soliton according to the spatial frequency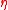 :
:
with
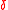 being the Dirac delta function
being the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
This corresponds to a modulus
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
(with the constant continuous background here omitted) :
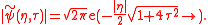
Quite interestingly, one can notice that for any given time
 , the modulus of the spectrum exhibits a typical triangular shape when plotted on a logarithmic scale. The broadest spectrum is obtained for
, the modulus of the spectrum exhibits a typical triangular shape when plotted on a logarithmic scale. The broadest spectrum is obtained for  , which corresponds to the maximum of compression of the spatio-temporal nonlinear structure.
, which corresponds to the maximum of compression of the spatio-temporal nonlinear structure.Experimental demonstration
Mathematical predictions by H. Peregrine had initially been established in the domain of hydrodynamics. This is however very different from where the Peregrine soliton has been for the first time experimentally generated and characterized.In 2010, more than 25 years after the initial work of Peregrine, researchers took advantage of the analogy that can be drawn between hydrodynamics and optics in order to generate Peregrine solitons in optical fiber
Optical fiber
An optical fiber is a flexible, transparent fiber made of a pure glass not much wider than a human hair. It functions as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of...
s. In fact, the evolution of light in fiber optics and the evolution of surface waves in deep water are both modelled by the nonlinear Schrödinger equation (note however that spatial and temporal variables have to be switched). Such an analogy has been exploited in the past in order to generate optical solitons
Soliton (optics)
In optics, the term soliton is used to refer to any optical field that does not change during propagation because of a delicate balance between nonlinear and linear effects in the medium. There are two main kinds of solitons:...
in optical fibers. Interestingly, by using exclusively standard optical communication
Optical communication
Optical communication is any form of telecommunication that uses light as the transmission medium.An optical communication system consists of a transmitter, which encodes a message into an optical signal, a channel, which carries the signal to its destination, and a receiver, which reproduces the...
components, it has been shown that even with an approximate initial condition (in the case of this work, an initial sinosoidal beating), a profile very close to the ideal Peregrine soliton can be generated. The typical triangular spectral shape has also been experimentally confirmed.
These results in optics have been confirmed in 2011 in hydrodynamics with experiments carried out in a 15-m long water wave tank. Other experiments carried out in the physics of plasmas
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
have also highlighted the emergence of Peregrine solitons in other fields ruled by the nonlinear Schrodinger equation .