Broyden's method
Encyclopedia
In numerical analysis, Broyden's method is a quasi-Newton method
for the numerical solution of nonlinear equations
in k variables. It was originally described by C. G. Broyden
in 1965.
Newton's method
for solving the equation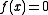
uses the Jacobian matrix and determinant, 
, at every iteration. However, computing this Jacobian is a difficult and expensive operation. The idea behind Broyden's method is to compute the whole Jacobian only at the first iteration, and to do a rank-one update at the other iterations.
In 1979 Gay proved that when Broyden's method is applied to a linear system of size n x n, it
terminates in 2n steps.
to multiple dimensions. The secant method replaces the first derivative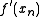
with the finite difference
approximation: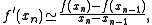
and proceeds in the Newton direction
:
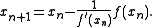
Broyden gives a generalization of this formula to a system of equations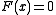
, replacing the derivative 
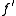with the Jacobian
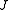. The Jacobian is determined using the secant equation (using the finite difference approximation):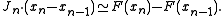
However this equation is under determined in more than one dimension. Broyden suggests using the current estimate of the Jacobian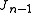
and improving upon it by taking the solution to the secant equation that is a minimal modification to 
(minimal in the sense of minimizing the Frobenius norm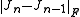 
):
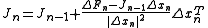
then proceeds in the Newton direction: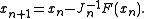
In the formula above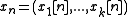
and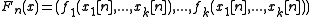 
are vector-columns with 
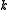elements for a system with k-dimensions. This way:
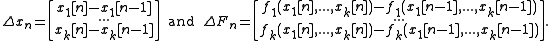
Broyden also suggested using the Sherman-Morrison formula
to update directly the inverse of the Jacobian: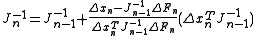
This method is commonly known as the "good Broyden's method". A similar technique can be derived by using a slightly different modification to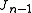
(which minimizes 
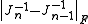instead); this yields the so-called "bad Broyden's method" (but see ):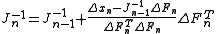
Many other quasi-Newton schemes have been suggested in optimization
, where one seeks a maximum or minimum by finding the root of the first derivative (gradient
in multi dimensions). The Jacobian of the gradient is called Hessian
and is symmetric, adding further constraints to its upgrade.
Quasi-Newton method
In optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
for the numerical solution of nonlinear equations
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
in k variables. It was originally described by C. G. Broyden
Charles George Broyden
Charles George Broyden was a mathematician who specialized in optimization problems and numerical linear algebra...
in 1965.
Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
for solving the equation
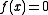uses the Jacobian matrix and determinant, 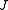, at every iteration. However, computing this Jacobian is a difficult and expensive operation. The idea behind Broyden's method is to compute the whole Jacobian only at the first iteration, and to do a rank-one update at the other iterations.In 1979 Gay proved that when Broyden's method is applied to a linear system of size n x n, it
terminates in 2n steps.
Description of the method
Broyden's method is a generalization of the secant methodSecant method
In numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite difference approximation of Newton's method. However, the method was developed...
to multiple dimensions. The secant method replaces the first derivative
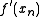with the finite differenceFinite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
approximation:
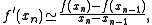
and proceeds in the Newton direction
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
:
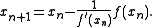
Broyden gives a generalization of this formula to a system of equations
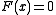, replacing the derivative 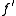with the JacobianJacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
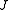. The Jacobian is determined using the secant equation (using the finite difference approximation):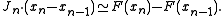However this equation is under determined in more than one dimension. Broyden suggests using the current estimate of the Jacobian
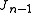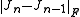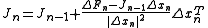
and improving upon it by taking the solution to the secant equation that is a minimal modification to (minimal in the sense of minimizing the Frobenius norm ):then proceeds in the Newton direction:
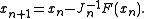
In the formula above
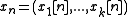and 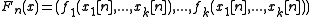are vector-columns with 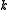elements for a system with k-dimensions. This way: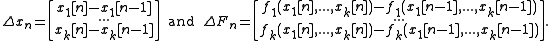Broyden also suggested using the Sherman-Morrison formula
Sherman-Morrison formula
In mathematics, in particular linear algebra, the Sherman–Morrison formula, named after Jack Sherman and Winifred J. Morrison, computes the inverse of the sum of an invertiblematrix Aand the dyadic product, u v^T,of a column vector u and a row vector v^T...
to update directly the inverse of the Jacobian:
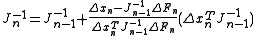
This method is commonly known as the "good Broyden's method". A similar technique can be derived by using a slightly different modification to
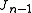(which minimizes 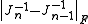instead); this yields the so-called "bad Broyden's method" (but see ):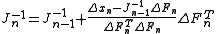Many other quasi-Newton schemes have been suggested in optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, where one seeks a maximum or minimum by finding the root of the first derivative (gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
in multi dimensions). The Jacobian of the gradient is called Hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
and is symmetric, adding further constraints to its upgrade.
See also
- Secant methodSecant methodIn numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite difference approximation of Newton's method. However, the method was developed...
- Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
- Quasi-Newton methodQuasi-Newton methodIn optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
- Newton's method in optimizationNewton's method in optimizationIn mathematics, Newton's method is an iterative method for finding roots of equations. More generally, Newton's method is used to find critical points of differentiable functions, which are the zeros of the derivative function.-Method:...
- Davidon-Fletcher-Powell formulaDavidon-Fletcher-Powell formulaThe Davidon–Fletcher–Powell formula finds the solution to the secant equation that is closest to the current estimate and satisfies the curvature condition . It was the first quasi-Newton method which generalize the secant method to a multidimensional problem...
- Broyden-Fletcher-Goldfarb-Shanno (BFGS) methodBFGS methodIn numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno method is a method for solving nonlinear optimization problems ....