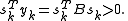Davidon-Fletcher-Powell formula
Encyclopedia
The Davidon–Fletcher–Powell formula (or DFP; named after William C. Davidon, Roger Fletcher, and Michael J. D. Powell
) finds the solution to the secant equation that is closest to the current estimate and satisfies the curvature condition (see below). It was the first quasi-Newton method
which generalize the secant method
to a multidimensional problem. This update maintains the symmetry and positive definiteness of the Hessian matrix
.
Given a function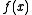
, its gradient
(
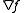), and positive definite Hessian matrix
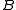, the Taylor series
is:
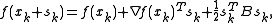
and the Taylor series
of the gradient itself (secant equation):
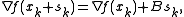
is used to update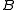
.
The DFP formula finds a solution that is symmetric, positive definite and closest to the current approximate value of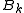
:
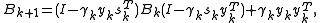
where
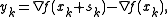
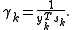
and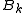
is a symmetric and positive definite matrix.
The corresponding update to the inverse Hessian approximation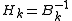
is given by:
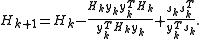
is assumed to be positive definite, and
the vectors
and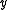 
must satisfy the curvature condition:
The DFP formula is quite effective, but it was soon superseded by the BFGS formula
, which is its dual (interchaning the roles of y and s).
Michael J. D. Powell
Michael James David Powell FRS, FIMA is a British mathematics Professor, retired from Cambridge University, where he earned his bachelors degree and, in 1979, his D.Sc. . He is known for his extensive work in numerical analysis, especially nonlinear optimization and Approximation...
) finds the solution to the secant equation that is closest to the current estimate and satisfies the curvature condition (see below). It was the first quasi-Newton method
Quasi-Newton method
In optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
which generalize the secant method
Secant method
In numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite difference approximation of Newton's method. However, the method was developed...
to a multidimensional problem. This update maintains the symmetry and positive definiteness of the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
.
Given a function
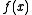, its gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
(
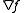), and positive definite Hessian matrixHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
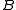, the Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
is:
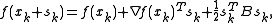
and the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of the gradient itself (secant equation):
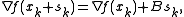
is used to update
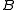.The DFP formula finds a solution that is symmetric, positive definite and closest to the current approximate value of
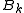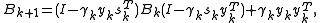
:where
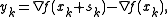
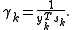
and
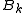is a symmetric and positive definite matrix.The corresponding update to the inverse Hessian approximation
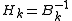is given by: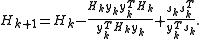 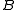is assumed to be positive definite, andthe vectors
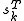and 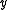must satisfy the curvature condition:
The DFP formula is quite effective, but it was soon superseded by the BFGS formula
BFGS method
In numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno method is a method for solving nonlinear optimization problems ....
, which is its dual (interchaning the roles of y and s).
See also
- Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
- Newton's method in optimizationNewton's method in optimizationIn mathematics, Newton's method is an iterative method for finding roots of equations. More generally, Newton's method is used to find critical points of differentiable functions, which are the zeros of the derivative function.-Method:...
- Quasi-Newton methodQuasi-Newton methodIn optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
- Broyden–Fletcher–Goldfarb–Shanno (BFGS) methodBFGS methodIn numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno method is a method for solving nonlinear optimization problems ....
- L-BFGS methodL-BFGSThe limited-memory BFGS algorithm is a member of the broad family of quasi-Newton optimization methods that uses a limited memory variation of the Broyden–Fletcher–Goldfarb–Shanno update to approximate the inverse Hessian matrix...
- SR1 formulaSR1 formulaThe Symmetric Rank 1 method is a quasi-Newton method to update the second derivative based on the derivatives calculated at two points...