
SR1 formula
Encyclopedia
The Symmetric Rank 1 method is a quasi-Newton method
to update the second derivative (Hessian)
based on the derivatives (gradients) calculated at two points. It is a generalization to the secant method
for a multidimensional problem.
This update maintains the symmetry of the matrix but does not guarantee that the update be positive definite.
The sequence of Hessian approximations generated by the SR1 method converges to the true Hessian under mild conditions, in theory; in practice, the approximate Hessians generated by the SR1 method show faster progress towards the true Hessian than do popular alternatives (BFGS or DFP
), in preliminary numerical experiments. The SR1 method has computational advantages for sparse or partially separable problems.
Alternative quasi-Newton methods like BFGS impose positive-definiteness, which is an inappropriate constraint on indefinite problems.
A twice continuously differentiable function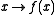 has a gradient
has a gradient
( ) and Hessian matrix
) and Hessian matrix
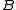 : The function
: The function 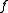 has an expansion as a Taylor series
has an expansion as a Taylor series
at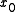 , which can be truncated
, which can be truncated
its gradient has a Taylor-series approximation also
which is used to update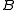 . The above secant-equation need not have a unique solution
. The above secant-equation need not have a unique solution 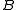 .
.
The SR1 formula computes (via an update of rank
1) the symmetric solution that is closest to the current approximate-value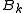 :
:
where
The corresponding update to the approximate inverse-Hessian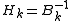 is
is
The SR1 formula has been rediscovered a number of times. A drawback is that the denominator can vanish. Some authors have suggested that the update be applied only if
where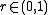 is a small number, e.g.
is a small number, e.g. 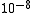 .
.
Quasi-Newton method
In optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
to update the second derivative (Hessian)
based on the derivatives (gradients) calculated at two points. It is a generalization to the secant method
Secant method
In numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite difference approximation of Newton's method. However, the method was developed...
for a multidimensional problem.
This update maintains the symmetry of the matrix but does not guarantee that the update be positive definite.
The sequence of Hessian approximations generated by the SR1 method converges to the true Hessian under mild conditions, in theory; in practice, the approximate Hessians generated by the SR1 method show faster progress towards the true Hessian than do popular alternatives (BFGS or DFP
Davidon-Fletcher-Powell formula
The Davidon–Fletcher–Powell formula finds the solution to the secant equation that is closest to the current estimate and satisfies the curvature condition . It was the first quasi-Newton method which generalize the secant method to a multidimensional problem...
), in preliminary numerical experiments. The SR1 method has computational advantages for sparse or partially separable problems.
Alternative quasi-Newton methods like BFGS impose positive-definiteness, which is an inappropriate constraint on indefinite problems.
A twice continuously differentiable function
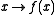 has a gradient
has a gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
(
 ) and Hessian matrix
) and Hessian matrixHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
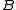 : The function
: The function 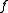 has an expansion as a Taylor series
has an expansion as a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
at
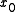 , which can be truncated
, which can be truncated
-
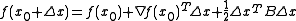 ;
;
its gradient has a Taylor-series approximation also
-
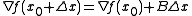 ,
,
which is used to update
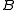 . The above secant-equation need not have a unique solution
. The above secant-equation need not have a unique solution 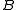 .
.The SR1 formula computes (via an update of rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
1) the symmetric solution that is closest to the current approximate-value
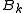 :
:
-
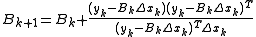 ,
,
where
-
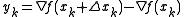 .
.
The corresponding update to the approximate inverse-Hessian
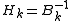 is
is
-
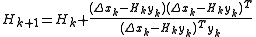 .
.
The SR1 formula has been rediscovered a number of times. A drawback is that the denominator can vanish. Some authors have suggested that the update be applied only if
-
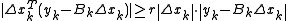 ,
,
where
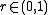 is a small number, e.g.
is a small number, e.g. 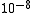 .
.See also
- Quasi-Newton methodQuasi-Newton methodIn optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
- Newton's method in optimizationNewton's method in optimizationIn mathematics, Newton's method is an iterative method for finding roots of equations. More generally, Newton's method is used to find critical points of differentiable functions, which are the zeros of the derivative function.-Method:...
- Broyden-Fletcher-Goldfarb-Shanno (BFGS) methodBFGS methodIn numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno method is a method for solving nonlinear optimization problems ....
- L-BFGS methodL-BFGSThe limited-memory BFGS algorithm is a member of the broad family of quasi-Newton optimization methods that uses a limited memory variation of the Broyden–Fletcher–Goldfarb–Shanno update to approximate the inverse Hessian matrix...

