Bruhat decomposition
Encyclopedia
In mathematics, the Bruhat decomposition (named after François Bruhat
) G = BWB into cells can be regarded as a general expression of the principle of Gauss–Jordan elimination
, which generically writes a matrix as a product of an upper triangular and lower triangular matrices—but with exceptional cases. It is related to the Schubert cell decomposition of Grassmannians: see Weyl group
for this.
More generally, any group with a (B,N) pair has a Bruhat decomposition.
The Bruhat decomposition of G is the decomposition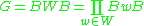
of G as a disjoint union of double coset
s of B parameterized by the elements of the Weyl group W. (Note that although W is not in general a subgroup of G, the coset wB is still well defined.)
GLn of invertible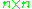
matrices with entries in some algebraically closed field, which is a reductive group. Then the Weyl group W is isomorphic to the symmetric group
Sn on n letters, with representatives the permutation matrices. In this case, we can take B to be the subgroup of upper triangular invertible matrices, so Bruhat decomposition says that one can write any invertible matrix A as a product U1PU2 where U1 and U2 are upper triangular, and P is a permutation matrix. Writing this as P = U1-1AU2-1, this says that any invertible matrix can be transformed into a permutation matrix via a series of row and column operations, where we are only allowed to add row i (resp. column i) to row j (resp. column j) if i>j (resp. i). The row operations correspond to U1-1, and the column operations correspond to U2-1.
The special linear group
SLn of invertible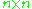
matrices with determinant
1 is a semisimple group
, and hence reductive. In this case, W is still isomorphic to the symmetric group Sn. However, the determinant of a permutation matrix is the sign of the permutation, so to represent an odd permutation in SLn, we can take one of the nonzero elements to be -1 instead of 1. Here B is the subgroup of upper triangular matrices with determinant 1, so the interpretation of Bruhat decomposition in this case is similar to the case of GLn.
of the word w in the Weyl group. Poincaré duality
constrains the topology of the cell decomposition, and thus the algebra of the Weyl group; for instance, the top dimensional cell is unique (it represents the fundamental class
), and corresponds to the longest element of a Coxeter group
.
François Bruhat
François Georges René Bruhat was a French mathematician who worked on algebraic groups. The Bruhat order of a Weyl group, the Bruhat decomposition, and the Schwartz–Bruhat functions are named after him....
) G = BWB into cells can be regarded as a general expression of the principle of Gauss–Jordan elimination
Gauss–Jordan elimination
In linear algebra, Gauss–Jordan elimination is an algorithm for getting matrices in reduced row echelon form using elementary row operations. It is a variation of Gaussian elimination. Gaussian elimination places zeros below each pivot in the matrix, starting with the top row and working downwards....
, which generically writes a matrix as a product of an upper triangular and lower triangular matrices—but with exceptional cases. It is related to the Schubert cell decomposition of Grassmannians: see Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
for this.
More generally, any group with a (B,N) pair has a Bruhat decomposition.
Definitions
- G is a connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, reductiveReductive groupIn mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
over an algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
. - B is a Borel subgroupBorel subgroupIn the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
of G - W is a Weyl group of G corresponding to a maximal torus of B.
The Bruhat decomposition of G is the decomposition
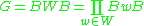
of G as a disjoint union of double coset
Double coset
In mathematics, an double coset in G, where G is a group and H and K are subgroups of G, is an equivalence class for the equivalence relation defined on G by...
s of B parameterized by the elements of the Weyl group W. (Note that although W is not in general a subgroup of G, the coset wB is still well defined.)
Examples
Let G be the general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GLn of invertible
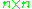matrices with entries in some algebraically closed field, which is a reductive group. Then the Weyl group W is isomorphic to the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn on n letters, with representatives the permutation matrices. In this case, we can take B to be the subgroup of upper triangular invertible matrices, so Bruhat decomposition says that one can write any invertible matrix A as a product U1PU2 where U1 and U2 are upper triangular, and P is a permutation matrix. Writing this as P = U1-1AU2-1, this says that any invertible matrix can be transformed into a permutation matrix via a series of row and column operations, where we are only allowed to add row i (resp. column i) to row j (resp. column j) if i>j (resp. i
The special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SLn of invertible
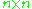matrices with determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1 is a semisimple group
Semisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
, and hence reductive. In this case, W is still isomorphic to the symmetric group Sn. However, the determinant of a permutation matrix is the sign of the permutation, so to represent an odd permutation in SLn, we can take one of the nonzero elements to be -1 instead of 1. Here B is the subgroup of upper triangular matrices with determinant 1, so the interpretation of Bruhat decomposition in this case is similar to the case of GLn.
Geometry
The cells in the Bruhat decomposition correspond to the Schubert cell decomposition of Grassmannians. The dimension of the cells corresponds to the lengthLength function
In mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
of the word w in the Weyl group. Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
constrains the topology of the cell decomposition, and thus the algebra of the Weyl group; for instance, the top dimensional cell is unique (it represents the fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
), and corresponds to the longest element of a Coxeter group
Longest element of a Coxeter group
In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
.
Computations
The number of cells in a given dimension of the Bruhat decomposition are the coefficients of the q-polynomial of the associated Dynkin diagram.See also
- Lie group decompositionsLie group decompositionsIn mathematics, Lie group decompositions, named after Sophus Lie, are used to analyse the structure of Lie groups and associated objects, by showing how they are built up out of subgroups. They are essential technical tools in the representation theory of Lie groups and Lie algebras; they can also...
- Birkhoff factorizationBirkhoff factorizationIn mathematics, Birkhoff factorization or Birkhoff decomposition, introduced by , is the factorization of an invertible matrix M with coefficients that are Laurent polynomials in z into a product M = M+M0M−, where M+ has entries that are polynomials in z, M0 is diagonal, and...
, a special case of the Bruhat decomposition for affine groups.