
Bumblebee models
Encyclopedia
Bumblebee models are effective field theories describing a vector field with a vacuum expectation value that spontaneously breaks Lorentz symmetry.
The development of bumblebee models was motivated primarily by the discovery that mechanisms in string theory (and subsequently other quantum theories of gravity) can lead to tensor-valued fields acquiring vacuum expectation values. Bumblebee models are different from local U(1) gauge theories. Nevertheless, in some bumblebee models, massless modes that behave like photon
s can appear. Bumblebee model is the simplest case of a theory with spontaneous Lorentz symmetry breaking.
and Stuart Samuel showed in 1989 that mechanisms arising in the context of string theory
can lead to spontaneous breaking of Lorentz symmetry. A set of models at the level of effective field theory were defined that contained gravitational fields and a vector field Bµ that has a nonzero vacuum expectation value,µ> = bµ . These have become known as bumblebee models.
Typically in these models, spontaneous Lorentz violation is caused by the presence of a potential term in the action. The vacuum value bµ, along with a background metric, give a solution that minimizes the bumblebee potential.
The vacuum value bµ acts as a fixed background field that spontaneously breaks Lorentz symmetry. It is an example, for the case of a vector, of a coefficient for Lorentz violation as defined in the Standard-Model Extension
.
The name bumblebee
model, coined by Kostelecký, is based on an insect whose ability to fly has sometimes been questioned on theoretical grounds, but which nonetheless is able to fly successfully.
kinetic terms for the gravitational and bumblebee fields, a potential V that induces spontaneous Lorentz breaking, and matter terms. In addition, there can be couplings between the gravitational, bumblebee, and matter fields.
One example, with conventional Einstein-Hilbert
and cosmological-constant terms for the gravity sector is the Lagrangian: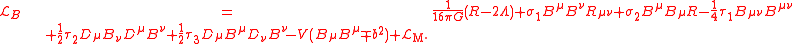
In this expression, is the covariant derivative,
is the covariant derivative,  , and the terms are controlled by a set of constants,
, and the terms are controlled by a set of constants,  ,
, 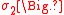 ,
,  ,
, 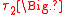 ,
,  . The matter-sector Lagrangian,
. The matter-sector Lagrangian, 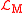 , can include couplings to Bµ.
, can include couplings to Bµ.
The potential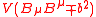 in this example is assumed to have a minimum when
in this example is assumed to have a minimum when

This condition is satisfied when the vector field has a vacuum value bµ obeying bµbµ = ±b2. The value of the constant ±b2 in the potential determines whether the vacuum vector is timelike, lightlike, or spacelike.
One commonly used example for the potential is a smooth quadratic function,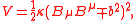
where is a constant. With this choice, a massive mode can appear in the theory for values of Bµ that do not minimize the potential V.
is a constant. With this choice, a massive mode can appear in the theory for values of Bµ that do not minimize the potential V.
Another common choice uses a Lagrange-multiplier field and is given as
In this case, the massive mode is frozen out. However, the Lagrange-multiplier field λ takes its place as an additional degree of freedom in the theory.
In the limit where the potential term V is removed from the theory, bumblebee models reduce to examples of vector-tensor theories of gravity.
The special Lagrangian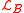 with
with 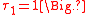 , and
, and  is the original type of model examined by Kostelecký and Samuel, known as the KS bumblebee model. The Lagrangian in this case has a Maxwell form for the bumblebee kinetic term, and is given as
is the original type of model examined by Kostelecký and Samuel, known as the KS bumblebee model. The Lagrangian in this case has a Maxwell form for the bumblebee kinetic term, and is given as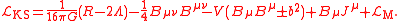
For this reason, Bµ can be thought of as a generalized vector potential, and interactions with a matter current can be included.
can be included.
The special Lagrangian with
with  ,
, 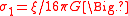 , and
, and  , is similar to the KS model, but includes nonminimal gravitational couplings parameterized by a coupling
, is similar to the KS model, but includes nonminimal gravitational couplings parameterized by a coupling  . The Lagrangian in this case is:
. The Lagrangian in this case is:
In all bumblebee models, the Lagrangian is invariant under both local Lorentz transformations and diffeomorphisms. A vierbein formalism can be used to introduce local components for the metric
, bumblebee, and matter fields at every spacetime
point. Spontaneous Lorentz violation occurs when the bumblebee field has a nonzero vacuum value in the local Lorentz frames.
The vierbein formalism is useful in expressing the structures of bumblebee theories. For example, it provides a natural way to express the direct link between spontaneous Lorentz breaking and diffeomorphism breaking. The spacetime vacuum value bµ is obtained when the vacuum solution for the vierbein acts on the local vacuum value for the vector field. The result is a fixed background field in the spacetime frame, which spontaneously breaks particle diffeomorphisms.
massive (Higgs) modes, and the possibility of a Higgs mechanism. In bumblebee models, Lorentz and diffeomorphism
symmetry
are spontaneously broken, so these effects have to be considered
in the context of both types of symmetry breaking
.
Nambu-Goldstone
modes appear when a continuous symmetry
is spontaneously broken. The Nambu-Goldstone
modes can be thought of as excitations generated by the broken symmetries that stay in the
degenerate vacuum of the theory. In contrast, massive (Higgs
) modes are excitations
that do not stay in the potential minimum. In this sense, the massive modes are orthogonal to the Nambu-Goldstone
excitations.
In bumblebee models, the excitations generated by the broken diffeomorphisms
are contained in both the vector field Bµ and the metric
gµν.
Different gauge choices can be made that effectively move the Nambu-Goldstone
degrees of freedom between these fields. For a wide range of models, including the KS bumblebee with a constant value of bµ, the diffeomorphism Nambu-Goldstone modes do not propagate as physical massless modes. Instead, they are auxiliary modes.
Different gauge choices also affect the interpretation of the Nambu-Goldstone modes that arise from spontaneous Lorentz breaking. In the most general bumblebee models, gauge fixing for the Lorentz transformations and diffeomorphisms can be made so that all of the Nambu-Goldstone modes are contained in the gravitational sector, either in the vierbein or, in some cases, in the metric
alone. With these choices, the bumblebee models are treated as
alternative theories of gravity.
For the general model with Lagrangian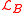 ,
,
with unrestricted values of the constants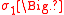 ,
, 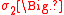 ,
,  ,
,  ,
, 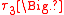 ,
,
the Nambu-Goldstone modes include both propagating massless modes and ghost modes.
One line of investigation is to search for restricted values of the parameters
that eliminate the ghosts as propagating modes.
In the KS bumblebee model, the only propagating Nambu-Goldstone
modes are two transverse massless modes, which have properties similar to the photon in an axial gauge. The propagating gravity modes describe the usual graviton modes
in general relativity.
In addition to the Nambu-Goldstone modes, there is a combined excitation in Bµ and gµν that does not stay in the potential minimum. It is a massive mode, similar to a Higgs excitation in the electroweak model
.
In KS bumblebee models, the massive-mode excitation acts as a background source of gravity and as a background source of charge density. The stability of the theory is affected by the behavior of the massive mode, which represents an additional degree of freedom compared to Einstein-Maxwell theory.
In the KS model, it can be shown that suitable initial conditions exist that set the massive mode to zero for all time. Alternatively, when the mass scale of the massive mode becomes large, its effects are greatly suppressed. In the limit of an infinite mass scale for the massive mode, the KS model is found to be equivalent to Einstein-Maxwell theory in a fixed axial gauge.
Note that other models besides the bumblebee allow known massless particles to arise as Nambu-Goldstone modes. For example, the cardinal model is based on a symmetric two-tensor. The Nambu-Goldstone modes resulting from spontaneous Lorentz breaking in this model can be equated with the graviton.
could emerge as Nambu-Goldstone modes
in a theory with spontaneous Lorentz violation first arose in the
context of special relativity
.
In 1951, Paul Dirac
considered a vector theory with a Lagrange-multiplier potential as an alternative model giving rise to the charge of the electron. It was later recognized that this was a theory with spontaneous Lorentz breaking.
Twelve years later, in 1963, James Bjorken
proposed a model in which collective excitations of a fermion field could lead to composite photons emerging as Nambu-Goldstone modes. The observable behavior of the photon in this original model was claimed to be equivalent to electrodynamics.
Subsequently, in 1968, Yoichiro Nambu
introduced a vector model that did not involve a symmetry-breaking potential. Instead, the constraint that the vector field have a fixed norm was introduced directly, and the resulting theory, which does not contain a massive mode, was shown to be equivalent to electromagnetism
in a fixed gauge.
The KS bumblebee model, which includes gravitational fields in addition to the vector field, extends the idea of photons arising as Nambu-Goldstone modes from special relativity
into general relativity
.
In the KS model, there is no local U(1) gauge symmetry. Instead, there are both massless Nambu-Goldstone modes and a massive mode as a result of spontaneous Lorentz violation. In the limit of infinite mass, the photon appears as massless Nambu-Goldstone modes.
arises when Lorentz symmetry is spontaneously broken. In the conventional gauge-theory Higgs mechanism
, the Nambu-Goldstone modes are reinterpreted as degrees of freedom associated with a massive gauge field. The Nambu-Goldstone modes are said to be eaten, while the gauge bosons gain a mass.
The possibility that a gravitational Higgs mechanism
in bumblebee models could endow the graviton
with mass was considered by Kostelecky and Samuel. They showed, however, that what appears to be a mass term involves the square of the affine connection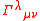 . Since the connection is a function of derivatives of the metric, this cannot be a mass term. Thus, there is no conventional Higgs mechanism
. Since the connection is a function of derivatives of the metric, this cannot be a mass term. Thus, there is no conventional Higgs mechanism
in bumblebee models that results in a massive graviton
.
This result assumed that the spacetime is a Riemann spacetime
. If instead a Riemann-Cartan spacetime is considered, then a Higgs mechanism
does become possible. However, in this case, it is not the graviton
that acquires a mass. Instead, it is the spin connection that becomes massive through spontaneous Lorentz breaking.
In Riemann-Cartan spacetime, covariant derivatives that act on local tensors involve the spin connection
. Since this type of geometry includes torsion
, the spin connection
provides an additional set of dynamical degrees of freedom that can propagate.
Bumblebee models in Riemann-Cartan spacetime lead to mass terms for the spin connection through spontaneous breaking of local Lorentz symmetry. The resulting Nambu-Goldstone modes can be reinterpreted, as in a Higgs mechanism
, as degrees of freedom that make the spin connection massive. However, finding suitable kinetic terms for the resulting massive spin connection
, free of ghosts and tachyon
s, remains an open problem.
The development of bumblebee models was motivated primarily by the discovery that mechanisms in string theory (and subsequently other quantum theories of gravity) can lead to tensor-valued fields acquiring vacuum expectation values. Bumblebee models are different from local U(1) gauge theories. Nevertheless, in some bumblebee models, massless modes that behave like photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s can appear. Bumblebee model is the simplest case of a theory with spontaneous Lorentz symmetry breaking.
Introduction
Alan KosteleckýAlan Kostelecký
Alan Kostelecký is a theoretical physicist who is currently a distinguished professor of physics at Indiana University, Bloomington. He is noted for his work on Lorentz symmetry breaking in particle physics...
and Stuart Samuel showed in 1989 that mechanisms arising in the context of string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
can lead to spontaneous breaking of Lorentz symmetry. A set of models at the level of effective field theory were defined that contained gravitational fields and a vector field Bµ that has a nonzero vacuum expectation value,
Typically in these models, spontaneous Lorentz violation is caused by the presence of a potential term in the action. The vacuum value bµ, along with a background metric, give a solution that minimizes the bumblebee potential.
The vacuum value bµ acts as a fixed background field that spontaneously breaks Lorentz symmetry. It is an example, for the case of a vector, of a coefficient for Lorentz violation as defined in the Standard-Model Extension
Standard-Model Extension
Standard-Model Extension is an effective field theory that contains the Standard Model, General Relativity, and all possible operators that break Lorentz symmetry.Violations of this fundamental symmetry can be studied within this general framework...
.
The name bumblebee
Bumblebee
A bumble bee is any member of the bee genus Bombus, in the family Apidae. There are over 250 known species, existing primarily in the Northern Hemisphere although they are common in New Zealand and in the Australian state of Tasmania.Bumble bees are social insects that are characterised by black...
model, coined by Kostelecký, is based on an insect whose ability to fly has sometimes been questioned on theoretical grounds, but which nonetheless is able to fly successfully.
Lagrangian
Different examples of bumblebee Lagrangians can be constructed. Their expressions includekinetic terms for the gravitational and bumblebee fields, a potential V that induces spontaneous Lorentz breaking, and matter terms. In addition, there can be couplings between the gravitational, bumblebee, and matter fields.
One example, with conventional Einstein-Hilbert
Einstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
and cosmological-constant terms for the gravity sector is the Lagrangian:
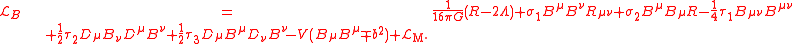
In this expression,
 is the covariant derivative,
is the covariant derivative,  , and the terms are controlled by a set of constants,
, and the terms are controlled by a set of constants,  ,
, 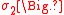 ,
,  ,
, 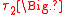 ,
,  . The matter-sector Lagrangian,
. The matter-sector Lagrangian, 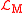 , can include couplings to Bµ.
, can include couplings to Bµ.The potential
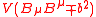 in this example is assumed to have a minimum when
in this example is assumed to have a minimum when
This condition is satisfied when the vector field has a vacuum value bµ obeying bµbµ = ±b2. The value of the constant ±b2 in the potential determines whether the vacuum vector is timelike, lightlike, or spacelike.
One commonly used example for the potential is a smooth quadratic function,
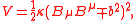
where
 is a constant. With this choice, a massive mode can appear in the theory for values of Bµ that do not minimize the potential V.
is a constant. With this choice, a massive mode can appear in the theory for values of Bµ that do not minimize the potential V.Another common choice uses a Lagrange-multiplier field and is given as

In this case, the massive mode is frozen out. However, the Lagrange-multiplier field λ takes its place as an additional degree of freedom in the theory.
In the limit where the potential term V is removed from the theory, bumblebee models reduce to examples of vector-tensor theories of gravity.
The special Lagrangian
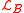 with
with 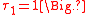 , and
, and  is the original type of model examined by Kostelecký and Samuel, known as the KS bumblebee model. The Lagrangian in this case has a Maxwell form for the bumblebee kinetic term, and is given as
is the original type of model examined by Kostelecký and Samuel, known as the KS bumblebee model. The Lagrangian in this case has a Maxwell form for the bumblebee kinetic term, and is given as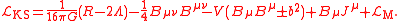
For this reason, Bµ can be thought of as a generalized vector potential, and interactions with a matter current
 can be included.
can be included.The special Lagrangian
 with
with  ,
, 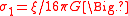 , and
, and  , is similar to the KS model, but includes nonminimal gravitational couplings parameterized by a coupling
, is similar to the KS model, but includes nonminimal gravitational couplings parameterized by a coupling  . The Lagrangian in this case is:
. The Lagrangian in this case is:
In all bumblebee models, the Lagrangian is invariant under both local Lorentz transformations and diffeomorphisms. A vierbein formalism can be used to introduce local components for the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
, bumblebee, and matter fields at every spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
point. Spontaneous Lorentz violation occurs when the bumblebee field has a nonzero vacuum value in the local Lorentz frames.
The vierbein formalism is useful in expressing the structures of bumblebee theories. For example, it provides a natural way to express the direct link between spontaneous Lorentz breaking and diffeomorphism breaking. The spacetime vacuum value bµ is obtained when the vacuum solution for the vierbein acts on the local vacuum value for the vector field. The result is a fixed background field in the spacetime frame, which spontaneously breaks particle diffeomorphisms.
Nambu-Goldstone and Massive Modes
Bumblebee models are useful for exploring the effects of spontaneous Lorentz violation in gravitational theories. These effects include the existence of Nambu-Goldstone modes,massive (Higgs) modes, and the possibility of a Higgs mechanism. In bumblebee models, Lorentz and diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
symmetry
are spontaneously broken, so these effects have to be considered
in the context of both types of symmetry breaking
Symmetry breaking
Symmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
.
Nambu-Goldstone
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
modes appear when a continuous symmetry
is spontaneously broken. The Nambu-Goldstone
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
modes can be thought of as excitations generated by the broken symmetries that stay in the
degenerate vacuum of the theory. In contrast, massive (Higgs
Higgs
The term Higgs appears in:* Alan Higgs, English businessman and philanthropist* Sir Derek Higgs, an English business leader and merchant banker* Eric Sidney Higgs, English archaeologist*Griffin Higgs...
) modes are excitations
that do not stay in the potential minimum. In this sense, the massive modes are orthogonal to the Nambu-Goldstone
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
excitations.
In bumblebee models, the excitations generated by the broken diffeomorphisms
are contained in both the vector field Bµ and the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
gµν.
Different gauge choices can be made that effectively move the Nambu-Goldstone
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
degrees of freedom between these fields. For a wide range of models, including the KS bumblebee with a constant value of bµ, the diffeomorphism Nambu-Goldstone modes do not propagate as physical massless modes. Instead, they are auxiliary modes.
Different gauge choices also affect the interpretation of the Nambu-Goldstone modes that arise from spontaneous Lorentz breaking. In the most general bumblebee models, gauge fixing for the Lorentz transformations and diffeomorphisms can be made so that all of the Nambu-Goldstone modes are contained in the gravitational sector, either in the vierbein or, in some cases, in the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
alone. With these choices, the bumblebee models are treated as
alternative theories of gravity.
For the general model with Lagrangian
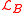 ,
,with unrestricted values of the constants
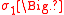 ,
, 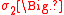 ,
,  ,
,  ,
, 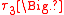 ,
,the Nambu-Goldstone modes include both propagating massless modes and ghost modes.
One line of investigation is to search for restricted values of the parameters
that eliminate the ghosts as propagating modes.
In the KS bumblebee model, the only propagating Nambu-Goldstone
modes are two transverse massless modes, which have properties similar to the photon in an axial gauge. The propagating gravity modes describe the usual graviton modes
in general relativity.
In addition to the Nambu-Goldstone modes, there is a combined excitation in Bµ and gµν that does not stay in the potential minimum. It is a massive mode, similar to a Higgs excitation in the electroweak model
Electroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
.
In KS bumblebee models, the massive-mode excitation acts as a background source of gravity and as a background source of charge density. The stability of the theory is affected by the behavior of the massive mode, which represents an additional degree of freedom compared to Einstein-Maxwell theory.
In the KS model, it can be shown that suitable initial conditions exist that set the massive mode to zero for all time. Alternatively, when the mass scale of the massive mode becomes large, its effects are greatly suppressed. In the limit of an infinite mass scale for the massive mode, the KS model is found to be equivalent to Einstein-Maxwell theory in a fixed axial gauge.
Note that other models besides the bumblebee allow known massless particles to arise as Nambu-Goldstone modes. For example, the cardinal model is based on a symmetric two-tensor. The Nambu-Goldstone modes resulting from spontaneous Lorentz breaking in this model can be equated with the graviton.
Photons from Spontaneous Lorentz Violation
The idea that the photonPhoton
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
could emerge as Nambu-Goldstone modes
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
in a theory with spontaneous Lorentz violation first arose in the
context of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
In 1951, Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
considered a vector theory with a Lagrange-multiplier potential as an alternative model giving rise to the charge of the electron. It was later recognized that this was a theory with spontaneous Lorentz breaking.
Twelve years later, in 1963, James Bjorken
James Bjorken
James Daniel "BJ" Bjorken is one of the world's foremost theoretical physicists. He was a Putnam Fellow in 1954, received a BS in physics from MIT in 1956, and obtained his PhD from Stanford University in 1959...
proposed a model in which collective excitations of a fermion field could lead to composite photons emerging as Nambu-Goldstone modes. The observable behavior of the photon in this original model was claimed to be equivalent to electrodynamics.
Subsequently, in 1968, Yoichiro Nambu
Yoichiro Nambu
is a Japanese-born American physicist, currently a professor at the University of Chicago. Known for his contributions to the field of theoretical physics, he was awarded a one-half share of the Nobel Prize in Physics in 2008 for the discovery of the mechanism of spontaneous broken symmetry in...
introduced a vector model that did not involve a symmetry-breaking potential. Instead, the constraint that the vector field have a fixed norm was introduced directly, and the resulting theory, which does not contain a massive mode, was shown to be equivalent to electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
in a fixed gauge.
The KS bumblebee model, which includes gravitational fields in addition to the vector field, extends the idea of photons arising as Nambu-Goldstone modes from special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
into general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
In the KS model, there is no local U(1) gauge symmetry. Instead, there are both massless Nambu-Goldstone modes and a massive mode as a result of spontaneous Lorentz violation. In the limit of infinite mass, the photon appears as massless Nambu-Goldstone modes.
Higgs mechanism
Because Lorentz symmetry is a local symmetry in the presence of gravity, the possibility of a Higgs mechanismHiggs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
arises when Lorentz symmetry is spontaneously broken. In the conventional gauge-theory Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
, the Nambu-Goldstone modes are reinterpreted as degrees of freedom associated with a massive gauge field. The Nambu-Goldstone modes are said to be eaten, while the gauge bosons gain a mass.
The possibility that a gravitational Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
in bumblebee models could endow the graviton
Graviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
with mass was considered by Kostelecky and Samuel. They showed, however, that what appears to be a mass term involves the square of the affine connection
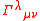 . Since the connection is a function of derivatives of the metric, this cannot be a mass term. Thus, there is no conventional Higgs mechanism
. Since the connection is a function of derivatives of the metric, this cannot be a mass term. Thus, there is no conventional Higgs mechanismHiggs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
in bumblebee models that results in a massive graviton
Graviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
.
This result assumed that the spacetime is a Riemann spacetime
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
. If instead a Riemann-Cartan spacetime is considered, then a Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
does become possible. However, in this case, it is not the graviton
Graviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
that acquires a mass. Instead, it is the spin connection that becomes massive through spontaneous Lorentz breaking.
In Riemann-Cartan spacetime, covariant derivatives that act on local tensors involve the spin connection
Spin connection
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the Levi-Civita connection...
. Since this type of geometry includes torsion
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
, the spin connection
Spin connection
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the Levi-Civita connection...
provides an additional set of dynamical degrees of freedom that can propagate.
Bumblebee models in Riemann-Cartan spacetime lead to mass terms for the spin connection through spontaneous breaking of local Lorentz symmetry. The resulting Nambu-Goldstone modes can be reinterpreted, as in a Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
, as degrees of freedom that make the spin connection massive. However, finding suitable kinetic terms for the resulting massive spin connection
Spin connection
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the Levi-Civita connection...
, free of ghosts and tachyon
Tachyon
A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph...
s, remains an open problem.
See also
- Standard-Model ExtensionStandard-Model ExtensionStandard-Model Extension is an effective field theory that contains the Standard Model, General Relativity, and all possible operators that break Lorentz symmetry.Violations of this fundamental symmetry can be studied within this general framework...
- Riemann-Cartan geometry
- Antimatter tests of Lorentz violationAntimatter tests of Lorentz violationHigh-precision experiments could revealsmall previously unseen differences between the behaviorof matter and antimatter.This prospect is appealing to physicists because it mayshow that nature is not Lorentz symmetric.- Introduction :...
- Lorentz-violating neutrino oscillationsLorentz-violating neutrino oscillationsLorentz-violating neutrino oscillation refers to the quantum phenomenon of neutrino oscillations described in a framework that allows the breakdown of Lorentz invariance...

