Bunyakovsky conjecture
Encyclopedia
The Bunyakovsky conjecture (or Bouniakowsky conjecture) stated in 1857 by the Russian
mathematician
Viktor Bunyakovsky
, claims that an irreducible polynomial
of degree two or higher with integer
coefficients generates for natural
arguments either an infinite set of numbers with greatest common divisor
(gcd) exceeding unity, or infinitely many prime number
s.
An example of the former case is the polynomial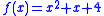
, which is irreducible but generates a set with gcd 2.
A conjectured example of the latter case is the polynomial f(x) = x2 + 1, for which some of the prime numbers generated are listed below:
The fifth Hardy–Littlewood conjecture—a special case of the Bunyakovsky conjecture—states that
generates infinitely many prime values for integer x > 1. To date, the Bunyakovsky conjecture has not been proven
correct, nor is a counterexample known.
The Bunyakovsky conjecture can be seen as an extension of Dirichlet's theorem
, which states that irreducible degree one polynomials always generate an infinite number of primes.
Russian Empire
The Russian Empire was a state that existed from 1721 until the Russian Revolution of 1917. It was the successor to the Tsardom of Russia and the predecessor of the Soviet Union...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Viktor Bunyakovsky
Viktor Bunyakovsky
Viktor Yakovlevich Bunyakovsky was a Russian mathematician, member and later vice president of the Petersburg Academy of Sciences.He worked in theoretical mechanics and number theory , and is credited with an early discovery of the Cauchy-Schwarz inequality, proving it for the infinite dimensional...
, claims that an irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
of degree two or higher with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients generates for natural
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
arguments either an infinite set of numbers with greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(gcd) exceeding unity, or infinitely many prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s.
An example of the former case is the polynomial
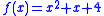, which is irreducible but generates a set with gcd 2.A conjectured example of the latter case is the polynomial f(x) = x2 + 1, for which some of the prime numbers generated are listed below:
| x | 1 | 2 | 4 | 6 | 10 | 14 | 16 | 20 | 24 | 26 | 36 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x2 + 1 | 2 | 5 | 17 | 37 | 101 | 197 | 257 | 401 | 577 | 677 | 1297 |
The fifth Hardy–Littlewood conjecture—a special case of the Bunyakovsky conjecture—states that
generates infinitely many prime values for integer x > 1. To date, the Bunyakovsky conjecture has not been provenMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
correct, nor is a counterexample known.
The Bunyakovsky conjecture can be seen as an extension of Dirichlet's theorem
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
, which states that irreducible degree one polynomials always generate an infinite number of primes.
See also
- Integer-valued polynomialInteger-valued polynomialIn mathematics, an integer-valued polynomial P is a polynomial taking an integer value P for every integer n. Certainly every polynomial with integer coefficients is integer-valued. There are simple examples to show that the converse is not true: for example the polynomialgiving the triangle...
- Cohn's irreducibility criterion
- Schinzel's hypothesis HSchinzel's hypothesis HIn mathematics, Schinzel's hypothesis H is a very broad generalisation of conjectures such as the twin prime conjecture. It aims to define the possible scope of a conjecture of the nature that several sequences of the type...
- Bateman–Horn conjecture
- Hardy and Littlewood's conjecture F