
Burau representation
Encyclopedia
In mathematics
the Burau representation is a representation
of the braid group
s, named after and originally studied by the German mathematician Werner Burau during the 1930s. The Burau representation has two common and near-equivalent formulations, the reduced and unreduced Burau representations.
 to be the mapping class group
to be the mapping class group
of a disc with n marked points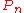 . The homology group
. The homology group  is free abelian of rank n. Moreover, the invariant subspace of
is free abelian of rank n. Moreover, the invariant subspace of 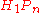 (under the action of
(under the action of  ) is primitive and infinite cyclic. Let
) is primitive and infinite cyclic. Let  be the projection onto this invariant subspace. Then there is a covering space
be the projection onto this invariant subspace. Then there is a covering space 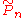 corresponding to this projection map. Much like in the construction of the Alexander polynomial
corresponding to this projection map. Much like in the construction of the Alexander polynomial
, consider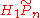 as a module over the group-ring of covering transformations
as a module over the group-ring of covering transformations 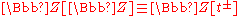 (a Laurent polynomial ring). As such a
(a Laurent polynomial ring). As such a  -module,
-module, 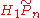 is free of rank n − 1. By the basic theory of covering spaces,
is free of rank n − 1. By the basic theory of covering spaces,  acts on
acts on  , and this representation is called the reduced Burau representation.
, and this representation is called the reduced Burau representation.
The unreduced Burau representation has a similar definition, namely one replaces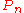 with its (real, oriented) blow-up
with its (real, oriented) blow-up
at the marked points. Then instead of considering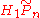 one considers the relative homology
one considers the relative homology 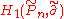 where
where 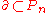 is the part of the boundary of
is the part of the boundary of 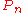 corresponding to the blow-up operation together with one point on the disc's boundary.
corresponding to the blow-up operation together with one point on the disc's boundary. 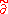 denotes the lift of
denotes the lift of  to
to 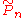 . As a
. As a  -module this is free of rank n.
-module this is free of rank n.
By the homology long exact sequence of a pair
, the Burau representations fit into a short exact sequence , where
, where 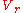 and
and 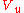 are reduced and unreduced Burau
are reduced and unreduced Burau  -modules respectively and
-modules respectively and  is the complement to the diagonal subspace (ie:
is the complement to the diagonal subspace (ie: 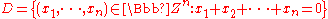 , and
, and  acts on
acts on 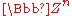 by the permutation representation.
by the permutation representation.
 is the closure of a braid
is the closure of a braid  , then the Alexander polynomial
, then the Alexander polynomial
is given by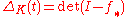 where
where  is the reduced Burau representation of the braid
is the reduced Burau representation of the braid  .
.
A more conceptual understanding interprets the linking or winding as coming from Poincaré duality
in first homology relative to the basepoint of a covering space, and uses the intersection form
(traditionally called Squier's Form as Craig Squier was the first to explore its properties). Stephen Bigelow combined computer techniques and the Long-Paton theorem to show that the Burau representation is not faithful for n ≥ 5 .
The Burau representation for n = 2, 3 has been known to be faithful for some time. The faithfulness of the Burau representation when n = 4 is an open problem.
. Moreover, when the variable is chosen to be a transcendental unit complex number
is chosen to be a transcendental unit complex number
near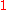 it is a positive-definite Hermitian pairing, thus the Burau representation can be thought of as a map into the Unitary group
it is a positive-definite Hermitian pairing, thus the Burau representation can be thought of as a map into the Unitary group
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Burau representation is a representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s, named after and originally studied by the German mathematician Werner Burau during the 1930s. The Burau representation has two common and near-equivalent formulations, the reduced and unreduced Burau representations.
Definition
Consider the braid groupBraid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
 to be the mapping class group
to be the mapping class groupMapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
of a disc with n marked points
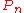 . The homology group
. The homology group  is free abelian of rank n. Moreover, the invariant subspace of
is free abelian of rank n. Moreover, the invariant subspace of 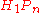 (under the action of
(under the action of  ) is primitive and infinite cyclic. Let
) is primitive and infinite cyclic. Let  be the projection onto this invariant subspace. Then there is a covering space
be the projection onto this invariant subspace. Then there is a covering space 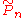 corresponding to this projection map. Much like in the construction of the Alexander polynomial
corresponding to this projection map. Much like in the construction of the Alexander polynomialAlexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
, consider
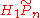 as a module over the group-ring of covering transformations
as a module over the group-ring of covering transformations 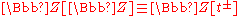 (a Laurent polynomial ring). As such a
(a Laurent polynomial ring). As such a  -module,
-module, 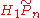 is free of rank n − 1. By the basic theory of covering spaces,
is free of rank n − 1. By the basic theory of covering spaces,  acts on
acts on  , and this representation is called the reduced Burau representation.
, and this representation is called the reduced Burau representation.The unreduced Burau representation has a similar definition, namely one replaces
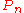 with its (real, oriented) blow-up
with its (real, oriented) blow-upBlowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
at the marked points. Then instead of considering
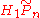 one considers the relative homology
one considers the relative homology 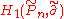 where
where 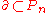 is the part of the boundary of
is the part of the boundary of 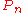 corresponding to the blow-up operation together with one point on the disc's boundary.
corresponding to the blow-up operation together with one point on the disc's boundary. 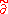 denotes the lift of
denotes the lift of  to
to 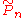 . As a
. As a  -module this is free of rank n.
-module this is free of rank n.By the homology long exact sequence of a pair
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
, the Burau representations fit into a short exact sequence
 , where
, where 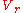 and
and 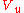 are reduced and unreduced Burau
are reduced and unreduced Burau  -modules respectively and
-modules respectively and  is the complement to the diagonal subspace (ie:
is the complement to the diagonal subspace (ie: 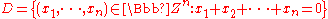 , and
, and  acts on
acts on 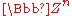 by the permutation representation.
by the permutation representation.Relation to the Alexander polynomial
If a knot is the closure of a braid
is the closure of a braid  , then the Alexander polynomial
, then the Alexander polynomialAlexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
is given by
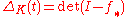 where
where  is the reduced Burau representation of the braid
is the reduced Burau representation of the braid  .
.Faithfulness
The first nonfaithful Burau representations are found without the use of computer, using a notion of winding number or contour integration.A more conceptual understanding interprets the linking or winding as coming from Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
in first homology relative to the basepoint of a covering space, and uses the intersection form
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
(traditionally called Squier's Form as Craig Squier was the first to explore its properties). Stephen Bigelow combined computer techniques and the Long-Paton theorem to show that the Burau representation is not faithful for n ≥ 5 .
The Burau representation for n = 2, 3 has been known to be faithful for some time. The faithfulness of the Burau representation when n = 4 is an open problem.
Geometry
Squier showed that the Burau representation preserves a sesquilinear formSesquilinear form
In mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
. Moreover, when the variable
 is chosen to be a transcendental unit complex number
is chosen to be a transcendental unit complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
near
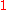 it is a positive-definite Hermitian pairing, thus the Burau representation can be thought of as a map into the Unitary group
it is a positive-definite Hermitian pairing, thus the Burau representation can be thought of as a map into the Unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
.

