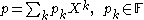Laurent polynomial
Encyclopedia
In mathematics
, a Laurent polynomial (named
after Pierre Alphonse Laurent
) in one variable over a field
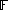 is a linear combination
is a linear combination
of positive and negative powers of the variable with coefficients in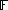 . Laurent polynomials in X form a ring
. Laurent polynomials in X form a ring
denoted [X, X−1]. They differ from ordinary polynomial
[X, X−1]. They differ from ordinary polynomial
s in that they may have terms of negative degree. The construction of Laurent polynomials may be iterated, leading to the ring of Laurent polynomials in several variables.
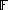 is an expression of the form
is an expression of the form
where X is a formal variable, the summation index k is an integer
(not necessarily positive) and only finitely many coefficients pk are non-zero. Two Laurent polynomials are equal if their coefficients are equal. Such expressions can be added, multiplied, and brought back to the same form by reducing similar terms. Formulas for addition and multiplication are exactly the same as for the ordinary polynomials, with the only difference that both positive and negative powers of X can be present:
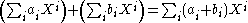
and
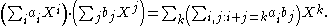
Since only finitely many coefficients ai and bj are non-zero, all sums in effect have only finitely many terms, and hence represent Laurent polynomials.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Laurent polynomial (named
after Pierre Alphonse Laurent
Pierre Alphonse Laurent
Pierre Alphonse Laurent was a French mathematician best known as the discoverer of the Laurent series, an expansion of a function into an infinite power series, generalizing the Taylor series expansion. He was born in Paris, France...
) in one variable over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
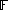 is a linear combination
is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of positive and negative powers of the variable with coefficients in
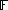 . Laurent polynomials in X form a ring
. Laurent polynomials in X form a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
denoted
 [X, X−1]. They differ from ordinary polynomial
[X, X−1]. They differ from ordinary polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in that they may have terms of negative degree. The construction of Laurent polynomials may be iterated, leading to the ring of Laurent polynomials in several variables.
Definition
A Laurent polynomial with coefficients in a field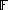 is an expression of the form
is an expression of the formwhere X is a formal variable, the summation index k is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
(not necessarily positive) and only finitely many coefficients pk are non-zero. Two Laurent polynomials are equal if their coefficients are equal. Such expressions can be added, multiplied, and brought back to the same form by reducing similar terms. Formulas for addition and multiplication are exactly the same as for the ordinary polynomials, with the only difference that both positive and negative powers of X can be present:
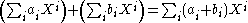
and
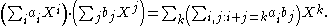
Since only finitely many coefficients ai and bj are non-zero, all sums in effect have only finitely many terms, and hence represent Laurent polynomials.
Properties
- A Laurent polynomial over C may be viewed as a Laurent seriesLaurent seriesIn mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
in which only finitely many coefficients are non-zero.
- The ring of Laurent polynomials R[X, X−1] is an extension of the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[X] obtained by "inverting X". More rigorously, it is the localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
in the multiplicative set consisting of the non-negative powers of X. Many properties of the Laurent polynomial ring follow from the general properties of localization.
- The ring of Laurent polynomials over a field is NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
(but not ArtinianArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
).
- If R is an integral domain, the units of the Laurent polynomial ring R[X, X−1] have the form uXk, where u is a unit of R and k is an integer. In particular, if K is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
then the units of K[X, X−1] have the form aXk, where a is a non-zero element of K.
- The Laurent polynomial ring R[X, X−1] is isomorphic to the group ringGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of the group Z of integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s over R. More generally, the Laurent polynomial ring in n variables is isomorphic to the group ring of the free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
of rank n. It follows that the Laurent polynomial ring can be endowed with a structure of a commutative, cocommutative Hopf algebraHopf algebraIn mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
.