
Bures metric
Encyclopedia
The Bures metric defines the infinitesimal distance between density matrix
operators defining quantum states, according to the following formula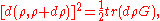
where is implicitly given by
is implicitly given by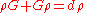
Some of the applications of the Bures metric include that given a target error, it allows the calculation of the minimum number of measurements to distinguish two different states and the use of the volume element as a candidate for the Jeffreys prior
probability density for mixed quantum states.
by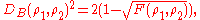
where the fidelity function is defined
as
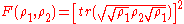
Another associated function is the Bures arc also known as Bures angle or Bures length defined as
which is a measure of the statistical distance between the quantum states.
be rewritten in terms of the variation of coordinate parameters as
where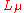 is the Symmetric Logarithmic Derivative operator (SLD) defined from
is the Symmetric Logarithmic Derivative operator (SLD) defined from
In this way, one has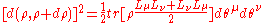
where the quantum Fisher metric (tensor components) is identified as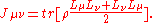
The definition of the SLD implies that the quantum Fisher metric is 4 times the Bures metric. In other words,
given that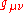 are components of the Bures metric tensor, one has
are components of the Bures metric tensor, one has
As it happens with the classical Fisher information metric, the quantum Fisher metric can be used
to find the Cramér–Rao bound of the covariance
.
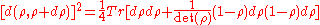

Another important formula is the one found by Hübner. This formula is written in terms of the eigenvectors and eigenvalues of the density matrix and reads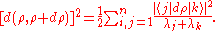

with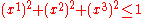 .
.
The components of the Bures metric in this parametrization can be calculated as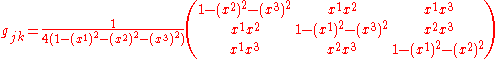 .
.
The Bures measure can be calculated by taking the square root of the determinant to find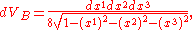
which can be used to calculate the Bures volume as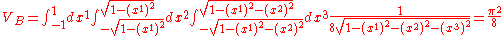
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
operators defining quantum states, according to the following formula
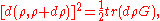
where
 is implicitly given by
is implicitly given by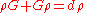
Some of the applications of the Bures metric include that given a target error, it allows the calculation of the minimum number of measurements to distinguish two different states and the use of the volume element as a candidate for the Jeffreys prior
Jeffreys prior
In Bayesian probability, the Jeffreys prior, named after Harold Jeffreys, is a non-informative prior distribution on parameter space that is proportional to the square root of the determinant of the Fisher information:...
probability density for mixed quantum states.
Bures Distance
The Bures distance is the finite version of the infinitesimal square distance described above and is givenby
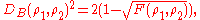
where the fidelity function is defined
as
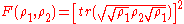
Another associated function is the Bures arc also known as Bures angle or Bures length defined as

which is a measure of the statistical distance between the quantum states.
Quantum Fisher Information
The Bures metric can be seen as the quantum equivalent of the Fisher information metric and canbe rewritten in terms of the variation of coordinate parameters as

where
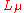 is the Symmetric Logarithmic Derivative operator (SLD) defined from
is the Symmetric Logarithmic Derivative operator (SLD) defined from
In this way, one has
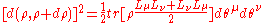
where the quantum Fisher metric (tensor components) is identified as
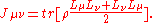
The definition of the SLD implies that the quantum Fisher metric is 4 times the Bures metric. In other words,
given that
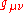 are components of the Bures metric tensor, one has
are components of the Bures metric tensor, one has
As it happens with the classical Fisher information metric, the quantum Fisher metric can be used
to find the Cramér–Rao bound of the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
.
Explicit Formulas
The actual computation of the Bures metric is not evident from the definition, so, some formulas were developed for that purpose. Dittmann obtained the following formulas for the quadratic form of the Bures metric, valid for 2x2 and 3x3 systems, respectively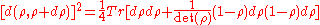

Another important formula is the one found by Hübner. This formula is written in terms of the eigenvectors and eigenvalues of the density matrix and reads
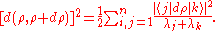
Two-Level System
The state of a two level system can be parametrized with three variables as
with
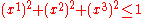 .
.The components of the Bures metric in this parametrization can be calculated as
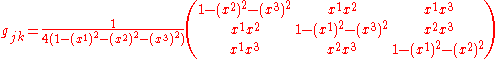 .
.The Bures measure can be calculated by taking the square root of the determinant to find
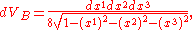
which can be used to calculate the Bures volume as
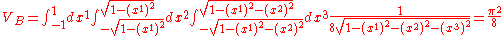
See also
- Fidelity of quantum statesFidelity of quantum statesIn quantum information theory, fidelity is a measure of the "closeness" of two quantum states. It is not a metric on the space of density matrices, but it can be used to define the Bures metric on this space.- Motivation :...
- Fisher informationFisher informationIn mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
- Fisher information metricFisher information metricIn information geometry, the Fisher information metric is a particular Riemannian metric which can be defined on a smooth statistical manifold, i.e., a smooth manifold whose points are probability measures defined on a common probability space....

