
Cake number
Encyclopedia
In mathematics, the cake number, denoted by Cn, is the maximum number of regions into which a 3-dimensional cube can be partitioned by exactly n planes. The cake number is so-called because one may imagine each partition of the cube by a plane as a slice made by a knife through a cube-shaped cake.
The values of Cn for increasing are given by
The cake numbers are the 3-dimensional analogue of the 2-dimensional lazy caterer's sequence
; the difference between successive cake numbers also gives the lazy caterer's sequence.
, and we denote the binomial coefficient
s by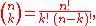
and we assume that n planes are available to partition the cube, then the number is:
The values of Cn for increasing are given by
The cake numbers are the 3-dimensional analogue of the 2-dimensional lazy caterer's sequence
Lazy caterer's sequence
The lazy caterer's sequence, more formally known as the central polygonal numbers, describes the maximum number of pieces of a circle that can be made with a given number of straight cuts. For example, three cuts across a pancake will produce six pieces if the cuts all meet at a common point, but...
; the difference between successive cake numbers also gives the lazy caterer's sequence.
General formula
If n! denotes the factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
, and we denote the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s by
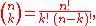
and we assume that n planes are available to partition the cube, then the number is:


