Calkin–Wilf tree
Encyclopedia
In number theory
, the Calkin–Wilf tree is a tree
in which the vertices correspond 1-for-1
to the positive rational number
s. The tree is rooted at the number 1, and any rational number expressed in simplest terms as the fraction
a/b has as its two children the numbers a/(a + b) and (a + b)/b. Every positive rational number appears exactly once in the tree.
The sequence of rational numbers in a breadth-first traversal
of the Calkin–Wilf tree is known as the Calkin–Wilf sequence. Its sequence of numerators (or, offset by one, denominators) is Stern's diatomic series, and can be computed by the fusc function.
The Calkin–Wilf tree is named after Neil Calkin and Herbert Wilf
, whose 2000 paper introduced it. Stern's diatomic series was formulated much earlier by Moritz Abraham Stern
, a 19th-century German mathematician who also invented the closely related Stern–Brocot tree.
of a and b is 1. If a/b < 1, the parent of a/b is a/(b − a); if a/b is greater than one, the parent of a/b is (a − b)/b. Thus, in either case, the parent is a fraction with a smaller sum of numerator and denominator, so repeated reduction of this type must eventually reach the number 1. As a graph with one outgoing edge per vertex and one root reachable by all other vertices, the Calkin–Wilf tree must indeed be a tree.
The children of any vertex in the Calkin–Wilf tree may be computed by inverting the formula for the parents of a vertex. Each vertex a/b has one child whose value is less than 1, a/(a + b), because this is the only value less than 1 whose parent formula leads back to a/b. Similarly, each vertex a/b has one child whose value is greater than 1, (a + b)/b.
Although it is a binary tree (each vertex has two children), the Calkin–Wilf tree is not a binary search tree
: its inorder does not coincide with the sorted order of its vertices. However, it is closely related to a different binary search tree on the same set of vertices, the Stern–Brocot tree: the vertices at each level of the two trees coincide, and are related to each other by a bit-reversal permutation.
Because the Calkin–Wilf tree contains every positive rational number exactly once, so does this sequence. The denominator of each fraction equals the numerator of the next fraction in the sequence.
The Calkin–Wilf sequence can also be generated directly by the formula
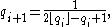
where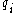
denotes the ith number in the sequence, starting from 
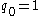, and 
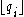represents the integral part.
The nth value in the sequence is the value fusc(n) of the fusc function,
defined by the recurrence relation
s fusc(2n) = fusc(n) and fusc(2n + 1) = fusc(n) + fusc(n + 1), with the base cases fusc(0) = 0 and fusc(1) = 1.
The nth rational number in a breadth-first traversal of the Calkin–Wilf tree is the number fusc(n) / fusc(n + 1). Thus, the diatomic sequence forms both the sequence of numerators and the sequence of denominators of the numbers in the Calkin–Wilf sequence.
The function fusc(n + 1) is the number of odd binomial coefficient
s of the form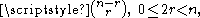
and
also counts the number of ways of writing n as a sum of powers of two
in which each power occurs at most twice. This can be seen from the recurrence defining fusc: the expressions as a sum of powers of two for an even number 2n either have no 1's in them (in which case they are formed by doubling each term an expression for n) or two 1's (in which case the rest of the expression is formed by doubling each term in an expression for n − 1), so the number of representations is the sum of the number of representations for n and for n − 1, matching the recurrence. Similarly, each representation for an odd number 2n + 1 is formed by doubling a representation for n and adding 1, again matching the recurrence. For instance,
has three representations as a sum of powers of with at most two copies of each power, so fusc(6 + 1) = 3.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Calkin–Wilf tree is a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
in which the vertices correspond 1-for-1
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
to the positive rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. The tree is rooted at the number 1, and any rational number expressed in simplest terms as the fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
a/b has as its two children the numbers a/(a + b) and (a + b)/b. Every positive rational number appears exactly once in the tree.
The sequence of rational numbers in a breadth-first traversal
Breadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
of the Calkin–Wilf tree is known as the Calkin–Wilf sequence. Its sequence of numerators (or, offset by one, denominators) is Stern's diatomic series, and can be computed by the fusc function.
The Calkin–Wilf tree is named after Neil Calkin and Herbert Wilf
Herbert Wilf
Herbert Saul Wilf is a mathematician, specializing in combinatorics and graph theory. He was the Thomas A. Scott Professor of Mathematics in Combinatorial Analysis and Computing at the University of Pennsylvania. He has written numerous books and research papers...
, whose 2000 paper introduced it. Stern's diatomic series was formulated much earlier by Moritz Abraham Stern
Moritz Abraham Stern
Moritz Abraham Stern was a German mathematician. Stern became Ordinarius at Göttingen University in 1858, succeeding Carl Friedrich Gauss. Stern was the first Jewish full professor at a German university....
, a 19th-century German mathematician who also invented the closely related Stern–Brocot tree.
Definition and structure
The Calkin–Wilf tree may be defined as a directed graph in which each positive rational number a/b occurs as a vertex and has one outgoing edge to another vertex, its parent. We assume that a/b is in simplest terms; that is, the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of a and b is 1. If a/b < 1, the parent of a/b is a/(b − a); if a/b is greater than one, the parent of a/b is (a − b)/b. Thus, in either case, the parent is a fraction with a smaller sum of numerator and denominator, so repeated reduction of this type must eventually reach the number 1. As a graph with one outgoing edge per vertex and one root reachable by all other vertices, the Calkin–Wilf tree must indeed be a tree.
The children of any vertex in the Calkin–Wilf tree may be computed by inverting the formula for the parents of a vertex. Each vertex a/b has one child whose value is less than 1, a/(a + b), because this is the only value less than 1 whose parent formula leads back to a/b. Similarly, each vertex a/b has one child whose value is greater than 1, (a + b)/b.
Although it is a binary tree (each vertex has two children), the Calkin–Wilf tree is not a binary search tree
Binary search tree
In computer science, a binary search tree , which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structurewhich has the following properties:...
: its inorder does not coincide with the sorted order of its vertices. However, it is closely related to a different binary search tree on the same set of vertices, the Stern–Brocot tree: the vertices at each level of the two trees coincide, and are related to each other by a bit-reversal permutation.
Breadth first traversal
The Calkin–Wilf sequence is the sequence of rational numbers generated by a breadth-first traversal of the Calkin–Wilf tree,- 1/1, 1/2, 2/1, 1/3, 3/2, 2/3, 3/1, 1/4, 4/3, 3/5, 5/2, 2/5, 5/3, 3/4, ….
Because the Calkin–Wilf tree contains every positive rational number exactly once, so does this sequence. The denominator of each fraction equals the numerator of the next fraction in the sequence.
The Calkin–Wilf sequence can also be generated directly by the formula
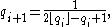
where
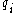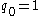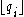denotes the ith number in the sequence, starting from , and represents the integral part.Stern's diatomic sequence
Stern's diatomic sequence is the integer sequenceInteger sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
- 0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, … .
The nth value in the sequence is the value fusc(n) of the fusc function,
defined by the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s fusc(2n) = fusc(n) and fusc(2n + 1) = fusc(n) + fusc(n + 1), with the base cases fusc(0) = 0 and fusc(1) = 1.
The nth rational number in a breadth-first traversal of the Calkin–Wilf tree is the number fusc(n) / fusc(n + 1). Thus, the diatomic sequence forms both the sequence of numerators and the sequence of denominators of the numbers in the Calkin–Wilf sequence.
The function fusc(n + 1) is the number of odd binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s of the form
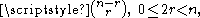andalso counts the number of ways of writing n as a sum of powers of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
in which each power occurs at most twice. This can be seen from the recurrence defining fusc: the expressions as a sum of powers of two for an even number 2n either have no 1's in them (in which case they are formed by doubling each term an expression for n) or two 1's (in which case the rest of the expression is formed by doubling each term in an expression for n − 1), so the number of representations is the sum of the number of representations for n and for n − 1, matching the recurrence. Similarly, each representation for an odd number 2n + 1 is formed by doubling a representation for n and adding 1, again matching the recurrence. For instance,
- 6 = 4 + 2 = 4 + 1 + 1 = 2 + 2 + 1 + 1
has three representations as a sum of powers of with at most two copies of each power, so fusc(6 + 1) = 3.