• In a coordinate space, and more generally in a free module, it refers to the standard basis defined by the Kronecker delta
• In a polynomial ring, it refers to its standard basis given by the monomial
  Monomial
  In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
  
  s, .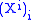
• For finite extension fields, it means the polynomial basis
  Polynomial basis
  In mathematics, the polynomial basis is a basis for finite extensions of finite fields.Let α ∈ GF be the root of a primitive polynomial of degree m over GF...
  
  .
• In representation theory, Lusztig's canonical basis and closely related Kashiwara's crystal basis in quantum groups and their representations

See also

• Canonical
  Canonical
  Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
  
  
• Canonical form
  Canonical form
  Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
  
  
• Normal form (disambiguation)
• Polynomial basis
  Polynomial basis
  In mathematics, the polynomial basis is a basis for finite extensions of finite fields.Let α ∈ GF be the root of a primitive polynomial of degree m over GF...
  
  
• Normal basis
  Normal basis
  In mathematics, a normal basis in field theory is a special kind of basis for Galois extensions of finite degree, characterised as forming a single orbit for the Galois group. The normal basis theorem states that any finite Galois extension of fields has a normal basis...
  
  
• Change of bases