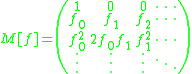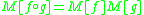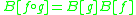Carleman matrix
Encyclopedia
In mathematics, a Carleman matrix is a matrix that is used to convert function composition
into matrix multiplication
. They are used in iteration theory to find the continuous iteration of functions that cannot be iterated by pattern recognition
alone. Other uses of Carleman matrices are in the theory of probability
generating functions, and Markov chains.
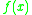 is defined as:
is defined as: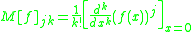
so as to satisfy the equation: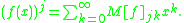
----
So for instance we have the computation of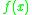 by
by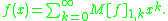
which is simply the dot-product of row 1 of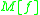 by a columnvector
by a columnvector 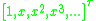
The entries of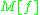 of the next row give the 2nd power of
of the next row give the 2nd power of 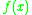 :
: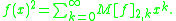
and also, for to have the zero'th power of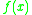 in
in 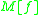 we assume the row 0 containing zeros everywhere except the first position, such that
we assume the row 0 containing zeros everywhere except the first position, such that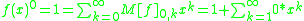
Thus the dot-product of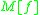 with the column-vector
with the column-vector 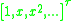 gives the columnvector
gives the columnvector 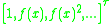
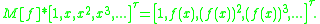
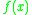 is defined as:
is defined as: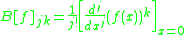
so as to satisfy the equation: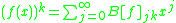
which means it is basically the transpose
of the Carleman matrix.
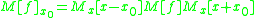
or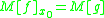 where
where 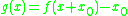 . This allows the matrix power to be related as:
. This allows the matrix power to be related as: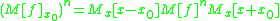
which makes the Carleman matrix M a (direct) representation of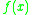 , and the Bell matrix B an anti-representation of
, and the Bell matrix B an anti-representation of 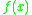 . Here the term
. Here the term 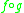 means the composition of functions
means the composition of functions 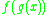
Other properties include:
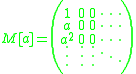
The Carleman matrix of the identity function is: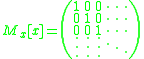
The Carleman matrix of a constant addition is: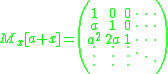
The Carleman matrix of a constant multiple is: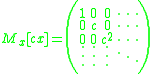
The Carleman matrix of a linear function is: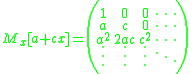
The Carleman matrix of a function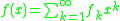 is:
is: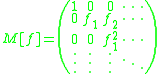
The Carleman matrix of a function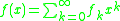 is:
is: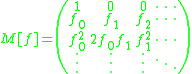
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
into matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. They are used in iteration theory to find the continuous iteration of functions that cannot be iterated by pattern recognition
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
alone. Other uses of Carleman matrices are in the theory of probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
generating functions, and Markov chains.
Definition
The Carleman matrix of a function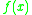 is defined as:
is defined as: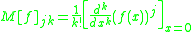
so as to satisfy the equation:
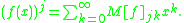
----
So for instance we have the computation of
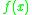 by
by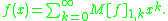
which is simply the dot-product of row 1 of
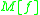 by a columnvector
by a columnvector 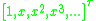
The entries of
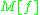 of the next row give the 2nd power of
of the next row give the 2nd power of 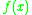 :
: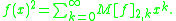
and also, for to have the zero'th power of
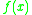 in
in 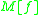 we assume the row 0 containing zeros everywhere except the first position, such that
we assume the row 0 containing zeros everywhere except the first position, such that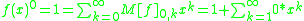
Thus the dot-product of
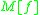 with the column-vector
with the column-vector 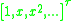 gives the columnvector
gives the columnvector 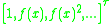
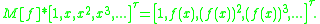
Bell matrix
The Bell matrix of a function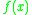 is defined as:
is defined as: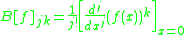
so as to satisfy the equation:
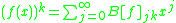
which means it is basically the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the Carleman matrix.
Generalization
A generalization of the Carleman matrix of a function can be defined around any point, such as: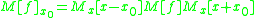
or
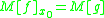 where
where 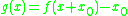 . This allows the matrix power to be related as:
. This allows the matrix power to be related as: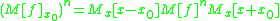
Matrix properties
These matrices satisfy the fundamental relationships:which makes the Carleman matrix M a (direct) representation of
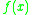 , and the Bell matrix B an anti-representation of
, and the Bell matrix B an anti-representation of 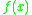 . Here the term
. Here the term 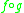 means the composition of functions
means the composition of functions 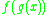
Other properties include:
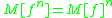 , where
, where 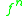 is function iteration and
is function iteration and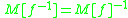 , where
, where 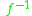 is the inverse functionInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
is the inverse functionInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
(if the Carleman matrix is invertible).
Examples
The Carleman matrix of a constant is: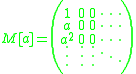
The Carleman matrix of the identity function is:
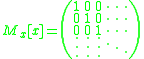
The Carleman matrix of a constant addition is:
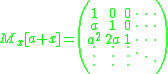
The Carleman matrix of a constant multiple is:
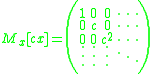
The Carleman matrix of a linear function is:
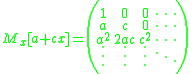
The Carleman matrix of a function
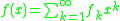 is:
is: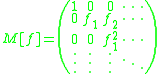
The Carleman matrix of a function
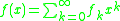 is:
is: