
Carleson measure
Encyclopedia
In mathematics
, a Carleson measure is a type of measure
on subset
s of n-dimension
al Euclidean space
Rn. Roughly speaking, a Carleson measure on a domain Ω is a measure that does not vanish at the boundary
of Ω when compared to the surface measure on the boundary
of Ω.
Carleson measures have many applications in harmonic analysis
and the theory of partial differential equations, for instance in the solution of Dirichlet problems with "rough" boundary. The Carleson condition is closely related to the boundedness of the Poisson operator. Carleson measures are named after the Swedish
mathematician
Lennart Carleson
.
(and hence measurable) set with non-empty boundary ∂Ω. Let μ be a Borel measure on Ω, and let σ denote the surface measure on ∂Ω. The measure μ is said to be a Carleson measure if there exists a constant C > 0 such that, for every point p ∈ ∂Ω and every radius r > 0,
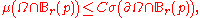
where
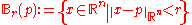
denotes the open ball of radius r about p.
on the boundary of D and let Lp(D, μ) denote the Lp space
on D with respect to the measure μ. Define the Poisson operator
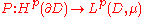
by
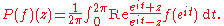
Then P is a bounded linear operator if and only if
the measure μ is Carleson.
of the set of constants C > 0 for which the Carleson condition
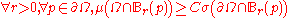
holds is known as the Carleson norm of the measure μ.
If C(R) is defined to be the infimum of the set of all constants C > 0 for which the restricted Carleson condition

holds, then the measure μ is said to satisfy the vanishing Carleson condition if C(R) → 0 as R → 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Carleson measure is a type of measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. Roughly speaking, a Carleson measure on a domain Ω is a measure that does not vanish at the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of Ω when compared to the surface measure on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of Ω.
Carleson measures have many applications in harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and the theory of partial differential equations, for instance in the solution of Dirichlet problems with "rough" boundary. The Carleson condition is closely related to the boundedness of the Poisson operator. Carleson measures are named after the Swedish
Sweden
Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Lennart Carleson
Lennart Carleson
Lennart Axel Edvard Carleson is a Swedish mathematician, known as a leader in the field of harmonic analysis.-Life:He was a student of Arne Beurling and received his Ph.D. from Uppsala University in 1950...
.
Definition
Let n ∈ N and let Ω ⊂ Rn be an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
(and hence measurable) set with non-empty boundary ∂Ω. Let μ be a Borel measure on Ω, and let σ denote the surface measure on ∂Ω. The measure μ is said to be a Carleson measure if there exists a constant C > 0 such that, for every point p ∈ ∂Ω and every radius r > 0,
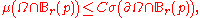
where
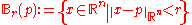
denotes the open ball of radius r about p.
Carleson's theorem on the Poisson operator
Let D denote the unit disc in the complex plane C, equipped with some Borel measure μ. For 1 ≤ p < +∞, let Hp(∂D) denote the Hardy spaceHardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
on the boundary of D and let Lp(D, μ) denote the Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
on D with respect to the measure μ. Define the Poisson operator
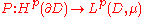
by
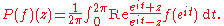
Then P is a bounded linear operator if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the measure μ is Carleson.
Other related concepts
The infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the set of constants C > 0 for which the Carleson condition
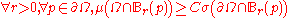
holds is known as the Carleson norm of the measure μ.
If C(R) is defined to be the infimum of the set of all constants C > 0 for which the restricted Carleson condition

holds, then the measure μ is said to satisfy the vanishing Carleson condition if C(R) → 0 as R → 0.

