
Castelnuovo–Mumford regularity
Encyclopedia
In algebraic geometry
, the Castelnuovo–Mumford regularity of a coherent sheaf
F over projective space
Pn is the smallest integer r such that it is r-regular, meaning that
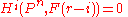
whenever i > 0. The regularity of a subscheme is defined to be the regularity of its sheaf of ideals. The regularity controls when the Hilbert function of the sheaf becomes a polynomial; more precisely dim H0(Pn, F(m)) is a polynomial in m when m is at least the regularity. The concept of r-regularity was introduced by , who attributed the following results to Guido Castelnuovo
:
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Castelnuovo–Mumford regularity of a coherent sheaf
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
F over projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Pn is the smallest integer r such that it is r-regular, meaning that
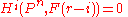
whenever i > 0. The regularity of a subscheme is defined to be the regularity of its sheaf of ideals. The regularity controls when the Hilbert function of the sheaf becomes a polynomial; more precisely dim H0(Pn, F(m)) is a polynomial in m when m is at least the regularity. The concept of r-regularity was introduced by , who attributed the following results to Guido Castelnuovo
Guido Castelnuovo
Guido Castelnuovo was an Italian mathematician. His father, Enrico Castelnuovo, was a novelist and campaigner for the unification of Italy...
:
- An r-regular sheaf is s-regular for any s ≥ r.
- If a coherent sheaf is r-regular then F(r) is generated by its global sections.

