Categorical algebra
Encyclopedia
In category theory
, a field of mathematics
, a categorical algebra is an associative algebra
, defined for any locally finite category
and commutative ring
with unity.
It generalizes the notions of group algebra
and incidence algebra
,
just as category
generalizes the notions of group
and partially ordered set
.
with unit.
Then as a set and as a module, the categorical algebra RC (or R[C]) is the free module
on the maps of C.
The multiplication on RC can be understood in several ways, depending on how one presents a free module.
Thinking of the free module as formal linear combinations (which are finite sums),
the multiplication is the multiplication (composition) of the category, where defined: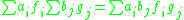
where
if their composition is not defined. This is defined for any finite sum.
Thinking of the free module as finitely supported functions,
the multiplication is defined as a convolution
: if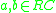
(thought of as functionals on the maps of C), then their product is defined as: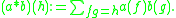
The latter sum is finite because the functions are finitely supported.
A locally finite category is one where every map can be written only finitely many ways as a product of non-identity maps.
The categorical algebra (in this sense) is defined as above, but allowing all coefficients to be non-zero.
In terms of formal sums, the elements are all formal sums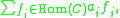
where there are no restrictions on the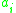
(they can all be non-zero).
In terms of functions, the elements are any functions from the maps of C to R, and multiplication is defined as convolution. The sum in the convolution is always finite because of the local finiteness assumption.
structure. Thus for a locally finite category, the dual of a categorical algebra (in the group algebra sense) is the categorical algebra (in the incidence algebra sense), and has both an algebra and coalgebra structure.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a field of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a categorical algebra is an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
, defined for any locally finite category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with unity.
It generalizes the notions of group algebra
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
and incidence algebra
Incidence algebra
In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
,
just as category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
generalizes the notions of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
.
Definition
Infinite categories are conventionally treated differently for group algebras and incidence algebras; the definitions agree for finite categories. We first present the definition that generalizes the group algebra.Group algebra-style definition
Let C be a category and R be a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with unit.
Then as a set and as a module, the categorical algebra RC (or R[C]) is the free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
on the maps of C.
The multiplication on RC can be understood in several ways, depending on how one presents a free module.
Thinking of the free module as formal linear combinations (which are finite sums),
the multiplication is the multiplication (composition) of the category, where defined:
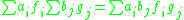
where
if their composition is not defined. This is defined for any finite sum.Thinking of the free module as finitely supported functions,
the multiplication is defined as a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
: if
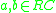(thought of as functionals on the maps of C), then their product is defined as: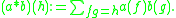The latter sum is finite because the functions are finitely supported.
Incidence algebra-style definition
The definition used for incidence algebras assumes that the category C is locally finite, is dual to the above definition, and defines a different object. This isn't a useful assumption for groups, as a group that is locally finite as a category is finite.A locally finite category is one where every map can be written only finitely many ways as a product of non-identity maps.
The categorical algebra (in this sense) is defined as above, but allowing all coefficients to be non-zero.
In terms of formal sums, the elements are all formal sums
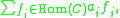
where there are no restrictions on the
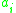(they can all be non-zero).In terms of functions, the elements are any functions from the maps of C to R, and multiplication is defined as convolution. The sum in the convolution is always finite because of the local finiteness assumption.
Dual
The module dual of the category algebra (in the group algebra sense of the definition) is the space of all maps from the maps of C to R, denoted F(C), and has a natural coalgebraCoalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
structure. Thus for a locally finite category, the dual of a categorical algebra (in the group algebra sense) is the categorical algebra (in the incidence algebra sense), and has both an algebra and coalgebra structure.
Examples
- If C is a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(thought of as a groupoidGroupoidIn mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
with a single object), then RC is the group algebraGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
. - If C is a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
(thought of as a category with a single object), then RC is the monoid ring. - If C is a partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
, then (using the appropriate definition), RC is the incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
.
External links
- Categorical Algebra at PlanetMath.
- Locally Finite Category at PlanetMath.