
Cauchy-Kovalevskaya theorem
Encyclopedia
In mathematics
, the Cauchy–Kowalevski theorem is the main local existence
and uniqueness theorem for analytic
partial differential equation
s associated with Cauchy initial value problems. A special case was proved by , and the full result by .
s. The theorem and its proof are valid for analytic functions of either real or complex variables.
Let K denote either the fields
of real or complex numbers, and let V=Km and W=Kn. Let A1, ..., An−1 be analytic function
s defined on some neighbourhood
of (0, 0) in V × W and taking values in the m × m matrices, and let b be an analytic function with values in V defined on the same neighbourhood. Then there is a neighbourhood of 0 in W on which the quasilinear Cauchy problem
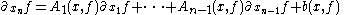
with initial condition
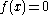
on the hypersurface
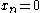
has a unique analytic solution ƒ : V → W near 0.
Lewy's example
shows that the theorem is not valid for all smooth functions.
The theorem can also be stated in abstract (real or complex) vector spaces. Let V and W be finite-dimensional real or complex vector spaces, with n = dim W. Let A1, ..., An−1 be analytic function
s with values in End (V)
and b an analytic function with values in V, defined on some neighbourhood
of (0, 0) in V × W. In this case, the same result holds.
can be expanded as formal power series
and give recurrence relations for the coefficients of the formal power series for f that uniquely determine the coefficients. The Taylor series
coefficients of the Ai's and b are majorized in matrix and vector norm by a simple scalar rational analytic function. The corresponding scalar Cauchy problem involving this function instead of the Ai's and b has an explicit local analytic solution. The absolute values of its coefficients majorize the norms of those of the original problem; so the formal power series solution must converge
where the scalar solution converges.

with initial conditions
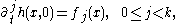
has a unique analytic solution near 0.
This follows from the first order problem by considering the derivatives of h appearing on the right hand side as components of a vector-valued function.

with the condition
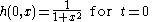
has a unique formal power series solution (expanded around (0, 0)). However this formal power series does not converge for any non-zero values of t, so there are no analytic solutions in a neighborhood of the origin. This shows that the condition |α| + j ≤ k above cannot be dropped. (This example is due to Kowalevski.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Cauchy–Kowalevski theorem is the main local existence
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
and uniqueness theorem for analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s associated with Cauchy initial value problems. A special case was proved by , and the full result by .
First order Cauchy–Kovalevski theorem
This theorem is about the existence of solutions to a system of m differential equations in n dimensions when the coefficients are analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s. The theorem and its proof are valid for analytic functions of either real or complex variables.
Let K denote either the fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of real or complex numbers, and let V=Km and W=Kn. Let A1, ..., An−1 be analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s defined on some neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of (0, 0) in V × W and taking values in the m × m matrices, and let b be an analytic function with values in V defined on the same neighbourhood. Then there is a neighbourhood of 0 in W on which the quasilinear Cauchy problem
Cauchy problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
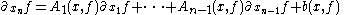
with initial condition
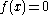
on the hypersurface
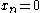
has a unique analytic solution ƒ : V → W near 0.
Lewy's example
Lewy's example
In the mathematical study of partial differential equations, Lewy's example is a celebrated example, due to Hans Lewy, of a linear partial differential equation with no solutions...
shows that the theorem is not valid for all smooth functions.
The theorem can also be stated in abstract (real or complex) vector spaces. Let V and W be finite-dimensional real or complex vector spaces, with n = dim W. Let A1, ..., An−1 be analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s with values in End (V)
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
and b an analytic function with values in V, defined on some neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of (0, 0) in V × W. In this case, the same result holds.
Proof by analytic majorization
Both sides of the partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
can be expanded as formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
and give recurrence relations for the coefficients of the formal power series for f that uniquely determine the coefficients. The Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
coefficients of the Ai's and b are majorized in matrix and vector norm by a simple scalar rational analytic function. The corresponding scalar Cauchy problem involving this function instead of the Ai's and b has an explicit local analytic solution. The absolute values of its coefficients majorize the norms of those of the original problem; so the formal power series solution must converge
where the scalar solution converges.
Higher-order Cauchy–Kovalevski theorem
If F and fj are analytic functions near 0, then the non-linear Cauchy problem
with initial conditions
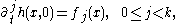
has a unique analytic solution near 0.
This follows from the first order problem by considering the derivatives of h appearing on the right hand side as components of a vector-valued function.
Example
The heat equationHeat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...

with the condition
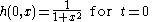
has a unique formal power series solution (expanded around (0, 0)). However this formal power series does not converge for any non-zero values of t, so there are no analytic solutions in a neighborhood of the origin. This shows that the condition |α| + j ≤ k above cannot be dropped. (This example is due to Kowalevski.)

