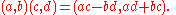In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Cayley–Dickson construction, named after Arthur Cayley

Arthur Cayley

Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....

 and Leonard Eugene Dickson

Leonard Eugene Dickson

Leonard Eugene Dickson was an American mathematician. He was one of the first American researchers in abstract algebra, in particular the theory of finite fields and classical groups, and is also remembered for a three-volume history of number theory.-Life:Dickson considered himself a Texan by...

, produces a sequence of algebras

Algebra over a field

In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...

  over the field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, each with twice the dimension of the previous one. The algebras produced by this process are known as Cayley–Dickson algebras; since they extend the complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s, they are hypercomplex number

Hypercomplex number

In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...

s.

These algebras all have an involution (or conjugate), with the product of an element and its conjugate (or sometimes the square root of this) called the norm.

For the first few steps, the next algebra loses a specific algebraic property.

More generally, the Cayley–Dickson construction takes any algebra with involution to another algebra with involution of twice the dimension.
The complex numbers can be written as ordered pair

Ordered pair

In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...

s (a, b) of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s a and b, with the addition operator being component-by-component and with multiplication defined by

A complex number whose second component is zero is associated with a real number: the complex number (a, 0) is the real number a.

Another important operation on complex numbers is conjugation.