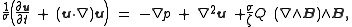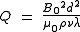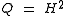Chandrasekhar number
Encyclopedia
The Chandrasekhar number is a dimensionless quantity
used in magnetic convection
to represent ratio of the Lorentz force
to the viscosity
. It is named after the India
n astrophysicist Subrahmanyan Chandrasekhar
.
The number's main function is as a measure of the magnetic field
, being proportional to the square of a characteristic magnetic field in a system.
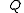 , and is motivated by a dimensionless form of the Navier-Stokes equation in the presence of a magnetic force in the equations of magnetohydrodynamics
, and is motivated by a dimensionless form of the Navier-Stokes equation in the presence of a magnetic force in the equations of magnetohydrodynamics
:
where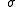 is the Prandtl number, and
is the Prandtl number, and 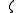 is the magnetic Prandtl number.
is the magnetic Prandtl number.
The Chandrasekhar number is thus defined as :
where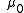 is the magnetic permeability,
is the magnetic permeability, 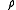 is the density
is the density
of the fluid, is the kinematic viscosity, and
is the kinematic viscosity, and  is the magnetic diffusivity
is the magnetic diffusivity
.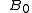 and
and 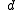 are a characteristic magnetic field and a length scale of the system respectively.
are a characteristic magnetic field and a length scale of the system respectively.
It is related to the Hartmann number
, , by the relation:
, by the relation:
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
used in magnetic convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
to represent ratio of the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
to the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. It is named after the India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
n astrophysicist Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar, FRS ) was an Indian origin American astrophysicist who, with William A. Fowler, won the 1983 Nobel Prize for Physics for key discoveries that led to the currently accepted theory on the later evolutionary stages of massive stars...
.
The number's main function is as a measure of the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, being proportional to the square of a characteristic magnetic field in a system.
Definition
The Chandrasekhar number is usually denoted by the letter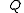 , and is motivated by a dimensionless form of the Navier-Stokes equation in the presence of a magnetic force in the equations of magnetohydrodynamics
, and is motivated by a dimensionless form of the Navier-Stokes equation in the presence of a magnetic force in the equations of magnetohydrodynamicsMagnetohydrodynamics
Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
:
where
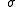 is the Prandtl number, and
is the Prandtl number, and 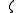 is the magnetic Prandtl number.
is the magnetic Prandtl number.The Chandrasekhar number is thus defined as :
where
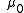 is the magnetic permeability,
is the magnetic permeability, 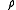 is the density
is the densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of the fluid,
 is the kinematic viscosity, and
is the kinematic viscosity, and  is the magnetic diffusivity
is the magnetic diffusivityDiffusivity
Diffusivity can refer to:*Diffusivity of heat*Diffusivity of mass:** Molecular diffusivity ** Eddy diffusivity*Momentum diffusivity...
.
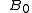 and
and 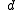 are a characteristic magnetic field and a length scale of the system respectively.
are a characteristic magnetic field and a length scale of the system respectively.It is related to the Hartmann number
Hartmann number
Hartmann number is the ratio of electromagnetic force to the viscous force first introduced by Hartmann. It is defined by:where* B is the magnetic field* L is the characteristic length scale* \sigma is the electrical conductivity* \mu is the viscosity...
,
 , by the relation:
, by the relation: