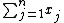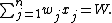Change-making problem
Encyclopedia
The change-making problem addresses the following question: how can a given amount of money be made with the least number of coins of given denominations? It is a knapsack type problem
, and has applications wider than just currency.
subject to
method)
of picking the largest denomination of coin which is not greater than the remaining amount to be made will always produce the optimal result. This is not automatically the case, though: if the coin denominations were 1, 3 and 4, then to make 6, the greedy algorithm would choose three coins (4,1,1) whereas the optimal solution is two coins (3,3).
Knapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
, and has applications wider than just currency.
Mathematical definition
Given a set of integer coin values {w1, w2, ..., wn} where w1 = 1 and wj < wj+1 for 1 ≤ j ≤ n − 1, and a positive integer W, find a set of non-negative integers {x1, x2, ..., xn} which minimizesubject to
Dynamic programming
Making a list of ways to make each amount from one upwards (an example of a dynamic programmingDynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
method)
Linear programming
Integer Linear Programming is often a quick way to solve this kind of problem, but the time it will take to resolve the problem is not certain, and may be slow in some casesGreedy method
In the US (and most other) coin systems, a greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
of picking the largest denomination of coin which is not greater than the remaining amount to be made will always produce the optimal result. This is not automatically the case, though: if the coin denominations were 1, 3 and 4, then to make 6, the greedy algorithm would choose three coins (4,1,1) whereas the optimal solution is two coins (3,3).