Chapman-Kolmogorov equation
Encyclopedia
In mathematics
, specifically in probability theory
and in particular the theory of Markovian stochastic process
es, the Chapman–Kolmogorov equation is an identity relating the joint probability distributions of different sets of coordinates on a stochastic process. The equation was arrived at independently by both the British mathematician Sydney Chapman
and the Russian mathematician Andrey Kolmogorov
.
Suppose that { fi } is an indexed collection of random variables, that is, a stochastic process. Let
be the joint probability density function of the values of the random variables f1 to fn. Then, the Chapman–Kolmogorov equation is
i.e. a straightforward marginalization over the nuisance variable
.
(Note that we have not yet assumed anything about the temporal (or any other) ordering of the random variables—the above equation applies equally to the marginalization of any of them.)
, the Chapman–Kolmogorov equation is equivalent to an identity on transition densities. In the Markov chain setting, one assumes that i1 < ... < in. Then, because of the Markov property
,
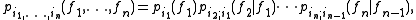
where the conditional probability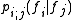
is the transition probability between the times 
. So, the Chapman–Kolmogorov equation takes the form
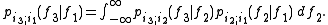
In English, and informally, this says that the probability of going from state 1 to state 3 can be found from the probabilities of going from 1 to an intermediate state 2 and then from 2 to 3, by adding up over all the possible intermediate states 2.
When the probability distribution on the state space of a Markov chain is discrete and the Markov chain is homogeneous, the Chapman–Kolmogorov equations can be expressed in terms of (possibly infinite-dimensional) matrix multiplication
, thus:
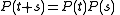
where P(t) is the transition matrix of jump t, i.e., P(t) is the matrix such that entry (i,j) contains the probability of the chain moving from state i to state j in t steps.
As a corollary, it follows that to calculate the transition matrix of jump t, it is sufficient to raise the transition matrix of jump one to the power of t, that is
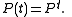
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and in particular the theory of Markovian stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es, the Chapman–Kolmogorov equation is an identity relating the joint probability distributions of different sets of coordinates on a stochastic process. The equation was arrived at independently by both the British mathematician Sydney Chapman
Sydney Chapman (astronomer)
Sydney Chapman FRS was a British mathematician and geophysicist. His work on the kinetic theory of gases, solar-terrestrial physics, and the Earth's ozone layer has inspired a broad range of research over many decades....
and the Russian mathematician Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
.
Suppose that { fi } is an indexed collection of random variables, that is, a stochastic process. Let
be the joint probability density function of the values of the random variables f1 to fn. Then, the Chapman–Kolmogorov equation is
i.e. a straightforward marginalization over the nuisance variable
Nuisance variable
In statistics, a nuisance parameter is any parameter which is not of immediate interest but which must be accounted for in the analysis of those parameters which are of interest...
.
(Note that we have not yet assumed anything about the temporal (or any other) ordering of the random variables—the above equation applies equally to the marginalization of any of them.)
Application to Markov chains
When the stochastic process under consideration is MarkovianMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
, the Chapman–Kolmogorov equation is equivalent to an identity on transition densities. In the Markov chain setting, one assumes that i1 < ... < in. Then, because of the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
,
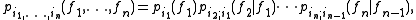
where the conditional probability
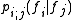is the transition probability between the times 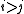. So, the Chapman–Kolmogorov equation takes the form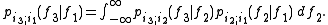In English, and informally, this says that the probability of going from state 1 to state 3 can be found from the probabilities of going from 1 to an intermediate state 2 and then from 2 to 3, by adding up over all the possible intermediate states 2.
When the probability distribution on the state space of a Markov chain is discrete and the Markov chain is homogeneous, the Chapman–Kolmogorov equations can be expressed in terms of (possibly infinite-dimensional) matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, thus:
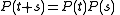
where P(t) is the transition matrix of jump t, i.e., P(t) is the matrix such that entry (i,j) contains the probability of the chain moving from state i to state j in t steps.
As a corollary, it follows that to calculate the transition matrix of jump t, it is sufficient to raise the transition matrix of jump one to the power of t, that is
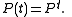
See also
- Fokker–Planck equation (also known as Kolmogorov forward equation)
- Kolmogorov backward equationKolmogorov backward equationThe Kolmogorov backward equation and its adjoint sometimes known as the Kolmogorov forward equation are partial differential equations that arise in the theory of continuous-time continuous-state Markov processes. Both were published by Andrey Kolmogorov in 1931...
- Examples of Markov chainsExamples of Markov chains- Board games played with dice :A game of snakes and ladders or any other game whose moves are determined entirely by dice is a Markov chain, indeed, an absorbing Markov chain. This is in contrast to card games such as blackjack, where the cards represent a 'memory' of the past moves. To see the...
- Master equationMaster equationIn physics and chemistry and related fields, master equations are used to describe the time-evolution of a system that can be modelled as being in exactly one of countable number of states at any given time, and where switching between states is treated probabilistically...
(physics)