Board games played with dice

A game of snakes and ladders

Snakes and ladders

Snakes and Ladders is an ancient Indian board game regarded today as a worldwide classic. It is played between two or more players on a game board having numbered, gridded squares. A number of "ladders" and "snakes" are pictured on the board, each connecting two specific board squares...

 or any other game whose moves are determined entirely by dice

Dice

A die is a small throwable object with multiple resting positions, used for generating random numbers...

 is a Markov chain, indeed, an absorbing Markov chain

Absorbing Markov chain

In the mathematical theory of probability, an absorbing Markov chain is a Markov chain in which every state can reach an absorbing state. An absorbing state is a state that, once entered, cannot be left....

. This is in contrast to card games such as blackjack, where the cards represent a 'memory' of the past moves. To see the difference, consider the probability for a certain event in the game. In the above mentioned dice games, the only thing that matters is the current state of the board. The next state of the board depends on the current state, and the next roll of the dice. It doesn't depend on how things got to their current state. In a game such as blackjack, a player can gain an advantage by remembering which cards have already been shown (and hence which cards are no longer in the deck), so the next state (or hand) of the game is not independent of the past states.

A center-biased random walk

Consider a random walk on the number line where, at each step, the position (call it x) may change by +1 (to the right) or -1 (to the left) with probabilities: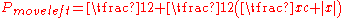





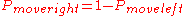
(where c is a constant greater than 0)
For example if the constant, c, equals 1, the probabilities of a move to the left at positions x = -2,-1,0,1,2 are given by 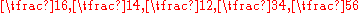respectively. The random walk has a centering effect that weakens as c increases.

Since the probabilities depend only on the current position (value of x) and not on any prior positions, this biased random walk satisfies the definition of a Markov chain.

A very simple weather model

The probabilities of weather conditions (modeled as either rainy or sunny), given the weather on the preceding day,
can be represented by a transition matrix:

The matrix P represents the weather model in which a sunny day is 90%
likely to be followed by another sunny day, and a rainy day is 50% likely to
be followed by another rainy day. The columns can be labelled "sunny" and
"rainy" respectively, and the rows can be labelled in the same order.

(P)_{i j} is the probability that, if a given day is of type i, it will be
followed by a day of type j.

Notice that the rows of P sum to 1: this is because P is a stochastic matrix

Stochastic matrix

In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...

.

Predicting the weather

The weather on day 0 is known to be sunny. This is represented by a vector in which the "sunny" entry is 100%, and the "rainy" entry is 0%:

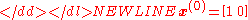
The weather on day 1 can be predicted by:

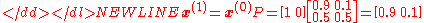
Thus, there is an 90% chance that day 1 will also be sunny.

The weather on day 2 can be predicted in the same way:

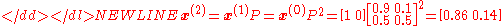
or

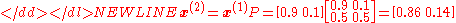
General rules for day n are:

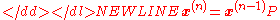
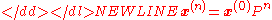
Steady state of the weather

In this example, predictions for the weather on more distant days are increasingly
inaccurate and tend towards a steady state vector. This vector represents
the probabilities of sunny and rainy weather on all days, and is independent
of the initial weather.

The steady state vector is defined as:



but only converges to a strictly positive vector if P is a regular

Regular matrix

Regular matrix may refer to:* regular stochastic matrix, a stochastic matrix such that all the entries of some power of the matrix are positive.* invertible matrix ....

 transition matrix (that is, there
is at least one Pⁿ with all non-zero entries).

Since the q is independent from initial conditions, it must be unchanged when transformed by P. This makes it an eigenvector (with eigenvalue 1), and means it can be derived from P. For the weather example:



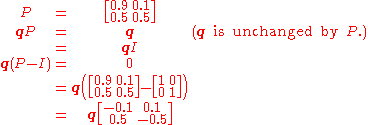
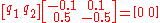
So

and since they are a probability vector we know that


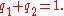
Solving this pair of simultaneous equations gives the steady state distribution:



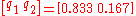
In conclusion, in the long term, 83% of days are sunny.

Citation ranking

Google

Google

Google Inc. is an American multinational public corporation invested in Internet search, cloud computing, and advertising technologies. Google hosts and develops a number of Internet-based services and products, and generates profit primarily from advertising through its AdWords program...

's page rank algorithm is essentially a Markov chain over the graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 of
the Web

World Wide Web

The World Wide Web is a system of interlinked hypertext documents accessed via the Internet...

. More information can be found in "The PageRank Citation Ranking: Bringing Order to the Web"
by Larry Page, Sergey Brin, R. Motwani, and T. Winograd .

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.