
Chapman–Robbins bound
Encyclopedia
In statistics
, the Chapman–Robbins bound or Hammersley–Chapman–Robbins bound is a lower bound on the variance
of estimator
s of a deterministic parameter. It is a generalization of the Cramér–Rao bound; compared to the Cramér–Rao bound, it is both tighter and applicable to a wider range of problems. However, it is usually more difficult to compute.
The bound was independently discovered by John Hammersley
in 1950, and by Douglas Chapman and Herbert Robbins
in 1951.
of X is given by p(x; θ). It is assumed that p(x; θ) is well-defined and that for all values of x and θ.
Suppose δ(X) is an unbiased
estimate of an arbitrary scalar function of θ, i.e.,
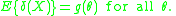
The Chapman–Robbins bound then states that

Note that the denominator in the lower bound above is exactly the -divergence of
-divergence of 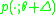 with respect to
with respect to 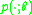 .
.
The Chapman–Robbins bound also holds under much weaker regularity conditions. For example, no assumption is made regarding differentiability of the probability density function p(x; θ). When p(x; θ) is non-differentiable, the Fisher information
is not defined, and hence the Cramér–Rao bound does not exist.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Chapman–Robbins bound or Hammersley–Chapman–Robbins bound is a lower bound on the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
s of a deterministic parameter. It is a generalization of the Cramér–Rao bound; compared to the Cramér–Rao bound, it is both tighter and applicable to a wider range of problems. However, it is usually more difficult to compute.
The bound was independently discovered by John Hammersley
John Hammersley
John Michael Hammersley was a British mathematician best known for his foundational work in the theory of self-avoiding walks and percolation theory. He was born in Helensburgh in Dunbartonshire, and educated at Sedbergh School. He started reading mathematics at Emmanuel College, Cambridge but was...
in 1950, and by Douglas Chapman and Herbert Robbins
Herbert Robbins
Herbert Ellis Robbins was an American mathematician and statistician who did research in topology, measure theory, statistics, and a variety of other fields. He was the co-author, with Richard Courant, of What is Mathematics?, a popularization that is still in print. The Robbins lemma, used in...
in 1951.
Statement
Let be an unknown, deterministic parameter, and let be a random variable, interpreted as a measurement of θ. Suppose the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of X is given by p(x; θ). It is assumed that p(x; θ) is well-defined and that for all values of x and θ.
Suppose δ(X) is an unbiased
Bias (statistics)
A statistic is biased if it is calculated in such a way that it is systematically different from the population parameter of interest. The following lists some types of, or aspects of, bias which should not be considered mutually exclusive:...
estimate of an arbitrary scalar function of θ, i.e.,
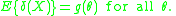
The Chapman–Robbins bound then states that

Note that the denominator in the lower bound above is exactly the
 -divergence of
-divergence of 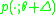 with respect to
with respect to 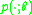 .
.Relation to Cramér–Rao bound
The Chapman–Robbins bound converges to the Cramér–Rao bound when , assuming the regularity conditions of the Cramér–Rao bound hold. This implies that, when both bounds exist, the Chapman–Robbins version is always at least as tight as the Cramér–Rao bound; in many cases, it is substantially tighter.The Chapman–Robbins bound also holds under much weaker regularity conditions. For example, no assumption is made regarding differentiability of the probability density function p(x; θ). When p(x; θ) is non-differentiable, the Fisher information
Fisher information
In mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
is not defined, and hence the Cramér–Rao bound does not exist.

