Character table
Encyclopedia
In group theory
, a character table is a two-dimensional table whose rows correspond to irreducible group representation
s, and whose columns correspond to classes of group elements. The entries consist of character
s, the trace
of the matrices representing group elements of the column's class in the given row's group representation.
In chemistry, crystallography, and spectroscopy, character tables of point groups are used to classify e.g. molecular vibrations according to their symmetry, and to predict whether a transition between two states is forbidden for symmetry reasons.
form a character table which encodes much useful information about the group
G in a compact form. Each row is labelled by an irreducible character and the entries in the row are the values of that character on the representatives of the respective conjugacy class
of G (because characters are class function
s). The columns are labelled by (representatives of) the conjugacy classes of G. It is customary to label the first row by the trivial character, and the first column by (the conjugacy class of) the identity
. The entries of the first column are the values of the irreducible characters at the identity, the degree
s of the irreducible characters. Characters of degree 1 are known as linear characters.
Here is the character table of C3 =
where ω is a primitive third root of unity.
The character table is always square, because the number of irreducible representations is equal to the number of conjugacy classes. The first row of the character table always consists of 1s, and corresponds to the trivial representation
(the 1-dimensional representation consisting of 1×1 matrices containing the entry 1).
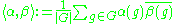
where
means the complex conjugate of the value of 
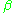on g. With respect to this inner product, the irreducible characters form an orthonormal basis
for the space of class-functions, and this yields the orthogonality relation for the rows of the character
table:
For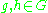
the orthogonality relation for columns is as follows:
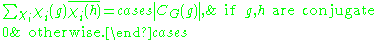
where the sum is over all of the irreducible characters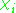
of G and the symbol 
denotes the order of the centralizer of 
.
The orthogonality relations can aid many computations including:
Certain properties of the group G can be deduced from its character table:
The character table does not in general determine the group up to
isomorphism
: for example, the quaternion group
Q and the dihedral group
of 8 elements (D4) have the same character table. Brauer asked whether the character table, together with the knowledge of how the powers of elements of its conjugacy classes are distributed, determines a finite group up to isomorphism. In 1964, this was answered in the negative by E. C. Dade.
The linear characters form a character group
, which has important number theoretic
connections.
which is non-trivial except for 2-groups, and outer because abelian groups are precisely those for which conjugation (inner automorphisms) acts trivially. In the example of 
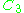above, this map sends 
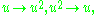and accordingly switches 
and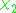 
(switching their values of 
and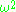 
). Note that this particular automorphism (negative in abelian groups) agrees with complex conjugation.
Formally, if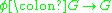
is an automorphism of G and 
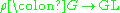is a representation, then 
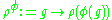is a representation. If 
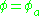is an inner automorphism
(conjugation by some element a), then it acts trivially on representations, because representations are class functions (conjugation does not change their value). Thus a given class of outer automorphisms, it acts on the characters – because inner automorphisms act trivially, the action of the automorphism group Aut descends to the quotient Out.
This relation can be used both ways: given an outer automorphism, one can produce new representations (if the representation is not equal on conjugacy classes that are interchanged by the outer automorphism), and conversely, one can restrict possible outer automorphisms based on the character table.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a character table is a two-dimensional table whose rows correspond to irreducible group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s, and whose columns correspond to classes of group elements. The entries consist of character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
s, the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the matrices representing group elements of the column's class in the given row's group representation.
In chemistry, crystallography, and spectroscopy, character tables of point groups are used to classify e.g. molecular vibrations according to their symmetry, and to predict whether a transition between two states is forbidden for symmetry reasons.
Definition and example
The irreducible complex characters of a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
form a character table which encodes much useful information about the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G in a compact form. Each row is labelled by an irreducible character and the entries in the row are the values of that character on the representatives of the respective conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
of G (because characters are class function
Class function
In mathematics, especially in the fields of group theory and representation theory of groups, a class function is a function f on a group G, such that f is constant on the conjugacy classes of G. In other words, f is invariant under the conjugation map on G...
s). The columns are labelled by (representatives of) the conjugacy classes of G. It is customary to label the first row by the trivial character, and the first column by (the conjugacy class of) the identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. The entries of the first column are the values of the irreducible characters at the identity, the degree
Degree (mathematics)
In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
s of the irreducible characters. Characters of degree 1 are known as linear characters.
Here is the character table of C3 =
| (1) | (u) | (u2) | |
| 1 | 1 | 1 | 1 |
| χ1 | 1 | ω | ω2 |
| χ2 | 1 | ω2 | ω |
where ω is a primitive third root of unity.
The character table is always square, because the number of irreducible representations is equal to the number of conjugacy classes. The first row of the character table always consists of 1s, and corresponds to the trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
(the 1-dimensional representation consisting of 1×1 matrices containing the entry 1).
Orthogonality relations
The space of complex-valued class functions of a finite group G has a natural inner-product: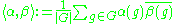where
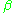means the complex conjugate of the value of on g. With respect to this inner product, the irreducible characters form an orthonormal basisfor the space of class-functions, and this yields the orthogonality relation for the rows of the character
table:
For
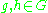the orthogonality relation for columns is as follows: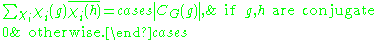where the sum is over all of the irreducible characters
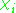of G and the symbol denotes the order of the centralizer of .The orthogonality relations can aid many computations including:
- Decomposing an unknown character as a linear combination of irreducible characters.
- Constructing the complete character table when only some of the irreducible characters are known.
- Finding the orders of the centralizers of representatives of the conjugacy classes of a group.
- Finding the order of the group.
Properties
Complex conjugation acts on the character table: since the complex conjugate of a representation is again a representation, the same is true for characters, and thus a character that takes on non-trivial complex values has a conjugate character.Certain properties of the group G can be deduced from its character table:
- The order of G is given by the sum of the squares of the entries of the first column (the degrees of the irreducible characters). (See Representation theory of finite groups#Applying Schur's lemma.) More generally, the sum of the squares of the absolute values of the entries in any column gives the order of the centralizer of an element of the corresponding conjugacy class.
- All normal subgroups of G (and thus whether or not G is simple) can be recognised from its character table. The kernelKernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of a character χ is the set of elements g in G for which χ(g) = χ(1); this is a normal subgroup of G. Each normal subgroup of G is the intersection of the kernels of some of the irreducible characters of G. - The derived subgroup of G is the intersection of the kernels of the linear characters of G. In particular, G is Abelian if and only if all its irreducible characters are linear.
- It follows, using some results of Richard BrauerRichard BrauerRichard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
from modular representation theoryModular representation theoryModular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
, that the prime divisors of the orders of the elements of each conjugacy class of a finite group can be deduced from its character table (an observation of Graham HigmanGraham HigmanGraham Higman FRS was a leading British mathematician. He is known for his contributions to group theory....
).
The character table does not in general determine the group up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
: for example, the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
Q and the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of 8 elements (D4) have the same character table. Brauer asked whether the character table, together with the knowledge of how the powers of elements of its conjugacy classes are distributed, determines a finite group up to isomorphism. In 1964, this was answered in the negative by E. C. Dade.
The linear characters form a character group
Character group
In mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory...
, which has important number theoretic
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
connections.
Outer automorphisms
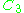The outer automorphism group acts on the character table by permuting columns (conjugacy classes) and accordingly rows, which gives another symmetry to the table. For example, abelian groups have the outer automorphism which is non-trivial except for 2-groups, and outer because abelian groups are precisely those for which conjugation (inner automorphisms) acts trivially. In the example of above, this map sends and accordingly switches and 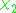(switching their values of and 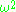). Note that this particular automorphism (negative in abelian groups) agrees with complex conjugation.Formally, if
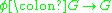is an automorphism of G and 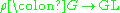is a representation, then 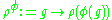is a representation. If 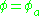is an inner automorphismInner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
(conjugation by some element a), then it acts trivially on representations, because representations are class functions (conjugation does not change their value). Thus a given class of outer automorphisms, it acts on the characters – because inner automorphisms act trivially, the action of the automorphism group Aut descends to the quotient Out.
This relation can be used both ways: given an outer automorphism, one can produce new representations (if the representation is not equal on conjugacy classes that are interchanged by the outer automorphism), and conversely, one can restrict possible outer automorphisms based on the character table.