Chase (algorithm)
Encyclopedia
The Chase is a simple fixpoint algorithm testing and enforcing implication of data dependencies in database systems. It plays important roles in database theory
as well as in practice.
It is used, directly or indirectly, on an everyday basis by people who design databases, and it is used in commercial systems to reason about the consistency and correctness of a data design. New applications of the chase in meta-data management and data exchange are still being discovered.
The Chase has its origins in two seminal papers, one by David Maier
, Alberto O. Mendelzon
, and Yehoshua Sagiv
and the other by
Alfred V. Aho, Catriel Beeri, and Jeffrey D. Ullman.
Chase test is for testing whether the projection of a relation onto any decomposition can be recovered by rejoining.
Let t be a tuple in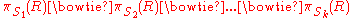
where R is a relation
and F is a set of functional dependencies
(FD). If tuples in R are represented as t1, ..., tk, the join of the projections of each ti should agree with t on
where i = 1, 2, ..., k. If ti is not on 
, the value is unknown.
Chase test can be done by drawing a tableau. Suppose R has attributes
A, B, ... and components of t are a, b, .... For ti use the same letter as t in the components that are in Si but subscript the letter with i if the component is not in i. Then, ti will agree with t if it is in Si and will have a unique value otherwise.
The first row represents S1. The components for attributes A and D are unsubscripted and those for attributes B and C are subscripted with i = 1. The second and third rows are filled in the same manner with S2 and S3 respectively.
The goal for this test is to use the given F to prove that t = (a, b, c, d) is really in R. To do so, the tableau can be chased by applying the FD’s in F to equate symbols in the tableau. Final tableau with a row that is the same as t implies that any tuple t in the join of the projections is actually a tuple of R.
To perform the chase test, first decompose all FD’s in F so each FD has a single attribute on the right hand side of the "arrow". F remains unchanged because all of its FD's already has a single attribute on the right hand side. F = {A→B, B→C, CD→A}.
When equating two symbols, if one of them is unsubscripted, make the other be the same so that the final tableau can have a row that is exactly the same as t = (a, b, c, d). Also, if both have their own subscript, change either to be the other. However, to avoid confusion, all of the occurrences should be changed.
First, apply A→B to the tableau. The first row is (a, b1, c1, d) where a is unsubscripted and b1 is subscripted with 1. Comparing the first row with the second one, change b2 to b1. Since the third row has a3, b in the third row stays the same. The resulting tableau is:
Then consider B→C. Both first and second rows have b1 and notice that the second row has an unsubscripted c. Therefore, the first row changes to (a, b1, c, d). Then the resulting tableau is:
Now consider CD→A. The first row has an unsubscripted c and an unsubscripted d, which is the same as in third row. This means that the A value for row one and three must be the same as well. Hence, change a3 in the third row to a. The resulting tableau is:
At this point, notice that the third row is (a, b, c, d) which is the same as t. Therefore, this is the final tableau for the chase test with given R and F. Hence, whenever R is projected onto S1, S2 and S3 and rejoined, the result is in R. Particularly, the resulting tuple is the same as the tuple of R that is projected onto {B, C, D}.
Database theory
Database theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems....
as well as in practice.
It is used, directly or indirectly, on an everyday basis by people who design databases, and it is used in commercial systems to reason about the consistency and correctness of a data design. New applications of the chase in meta-data management and data exchange are still being discovered.
The Chase has its origins in two seminal papers, one by David Maier
David Maier
David Maier is a professor of computer science at Portland State University.He has been chairman of the program committee of ACM SIGMOD. He also served as an associate editor of ACM Transactions on Database Systems...
, Alberto O. Mendelzon
Alberto O. Mendelzon
Alberto O. Mendelzon was an Argentine-Canadian computer scientist who died on June 16, 2005.Alberto Mendelzon was born in Buenos Aires, Argentina. He received a Ph.D. degree from Princeton University in 1979, where his advisor was Jeffrey Ullman. After that he was a post-doctoral fellow at the IBM...
, and Yehoshua Sagiv
Yehoshua Sagiv
Yehoshua Chaim Sagiv is a computer scientist and professor of computer science at the Hebrew University of Jerusalem. He obtained his PhD at Princeton University in 1978...
and the other by
Alfred V. Aho, Catriel Beeri, and Jeffrey D. Ullman.
Chase test is for testing whether the projection of a relation onto any decomposition can be recovered by rejoining.
Let t be a tuple in
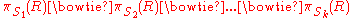where R is a relationRelation (database)
In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
and F is a set of functional dependencies
Functional dependency
A functional dependency is a constraint between two sets of attributes in a relation from a database.Given a relation R, a set of attributes X in R is said to functionally determine another attribute Y, also in R, if, and only if, each X value is associated with precisely one Y value...
(FD). If tuples in R are represented as t1, ..., tk, the join of the projections of each ti should agree with t on
where i = 1, 2, ..., k. If ti is not on , the value is unknown.Chase test can be done by drawing a tableau. Suppose R has attributes
Attribute (computing)
In computing, an attribute is a specification that defines a property of an object, element, or file. It may also refer to or set the specific value for a given instance of such....
A, B, ... and components of t are a, b, .... For ti use the same letter as t in the components that are in Si but subscript the letter with i if the component is not in i. Then, ti will agree with t if it is in Si and will have a unique value otherwise.
Example
Suppose R(A, B, C, D) which are decomposed into relations with attributes S1 = {A, D}, S2 = {A, C} and S3 = {B, C, D} and F = {A→B, B→C, CD→A} is given. The initial tableau for this decomposition is:| A | B | C | D |
|---|---|---|---|
| a | b1 | c1 | d |
| a | b2 | c | d2 |
| a3 | b | c | d |
The first row represents S1. The components for attributes A and D are unsubscripted and those for attributes B and C are subscripted with i = 1. The second and third rows are filled in the same manner with S2 and S3 respectively.
The goal for this test is to use the given F to prove that t = (a, b, c, d) is really in R. To do so, the tableau can be chased by applying the FD’s in F to equate symbols in the tableau. Final tableau with a row that is the same as t implies that any tuple t in the join of the projections is actually a tuple of R.
To perform the chase test, first decompose all FD’s in F so each FD has a single attribute on the right hand side of the "arrow". F remains unchanged because all of its FD's already has a single attribute on the right hand side. F = {A→B, B→C, CD→A}.
When equating two symbols, if one of them is unsubscripted, make the other be the same so that the final tableau can have a row that is exactly the same as t = (a, b, c, d). Also, if both have their own subscript, change either to be the other. However, to avoid confusion, all of the occurrences should be changed.
First, apply A→B to the tableau. The first row is (a, b1, c1, d) where a is unsubscripted and b1 is subscripted with 1. Comparing the first row with the second one, change b2 to b1. Since the third row has a3, b in the third row stays the same. The resulting tableau is:
| A | B | C | D |
|---|---|---|---|
| a | b1 | c1 | d |
| a | b1 | c | d2 |
| a3 | b | c | d |
Then consider B→C. Both first and second rows have b1 and notice that the second row has an unsubscripted c. Therefore, the first row changes to (a, b1, c, d). Then the resulting tableau is:
| A | B | C | D |
|---|---|---|---|
| a | b1 | c | d |
| a | b1 | c | d2 |
| a3 | b | c | d |
Now consider CD→A. The first row has an unsubscripted c and an unsubscripted d, which is the same as in third row. This means that the A value for row one and three must be the same as well. Hence, change a3 in the third row to a. The resulting tableau is:
| A | B | C | D |
|---|---|---|---|
| a | b1 | c | d |
| a | b1 | c | d2 |
| a | b | c | d |
At this point, notice that the third row is (a, b, c, d) which is the same as t. Therefore, this is the final tableau for the chase test with given R and F. Hence, whenever R is projected onto S1, S2 and S3 and rejoined, the result is in R. Particularly, the resulting tuple is the same as the tuple of R that is projected onto {B, C, D}.