Chern-Simons form
Encyclopedia
In mathematics
, the Chern–Simons forms are certain secondary characteristic class
es. They have been found to be of interest in gauge theory
, and they (especially the 3-form) define the action of Chern–Simons theory. The theory is named for Shiing-Shen Chern
and James Harris Simons
, co-authors of a 1974 paper entitled "Characteristic Forms and Geometric Invariants," from which the theory arose.
and a Lie algebra
valued 1-form,
over it, we can define a family of p-forms:
In one dimension, the Chern–Simons 1-form is given by
In three dimensions, the Chern–Simons 3-form is given by
In five dimensions, the Chern–Simons 5-form is given by
where the curvature F is defined as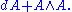
The general Chern–Simons form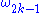
is defined in such a way that
where the wedge product is used to define Fk.
See gauge theory
for more details.
In general, the Chern–Simons p-form is defined for any odd p. See gauge theory
for the definitions. Its integral
over a p-dimensional manifold
is a global geometric invariant, and is typically gauge invariant modulo addition of an integer.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Chern–Simons forms are certain secondary characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es. They have been found to be of interest in gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, and they (especially the 3-form) define the action of Chern–Simons theory. The theory is named for Shiing-Shen Chern
Shiing-Shen Chern
Shiing-Shen Chern was a Chinese American mathematician, one of the leaders in differential geometry of the twentieth century.-Early years in China:...
and James Harris Simons
James Harris Simons
James Harris "Jim" Simons is an American hedge fund manager, mathematician, and philanthropist.In 1982, Simons founded Renaissance Technologies, a private investment firm based in New York with over $15 billion under management; Simons is still at the helm, as CEO, of what is now one of the...
, co-authors of a 1974 paper entitled "Characteristic Forms and Geometric Invariants," from which the theory arose.
Definition
Given a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
and a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
valued 1-form,
over it, we can define a family of p-forms:In one dimension, the Chern–Simons 1-form is given by
In three dimensions, the Chern–Simons 3-form is given by
In five dimensions, the Chern–Simons 5-form is given by
where the curvature F is defined as
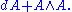
The general Chern–Simons form
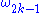is defined in such a way thatwhere the wedge product is used to define Fk.
See gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
for more details.
In general, the Chern–Simons p-form is defined for any odd p. See gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
for the definitions. Its integral
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
over a p-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is a global geometric invariant, and is typically gauge invariant modulo addition of an integer.
See also
- Chern–Weil homomorphism
- Chiral anomalyChiral anomalyA chiral anomaly is the anomalous nonconservation of a chiral current. In some theories of fermions with chiral symmetry, the quantization may lead to the breaking of this chiral symmetry. In that case, the charge associated with the chiral symmetry is not conserved.The non-conservation happens...
- Topological quantum field theoryTopological quantum field theoryA topological quantum field theory is a quantum field theory which computes topological invariants....
- Jones polynomial