
Chevalley basis
Encyclopedia
In mathematics, a Chevalley basis for a simple
complex
Lie algebra
is
a basis
constructed by Claude Chevalley
with the property that all structure constants are integers. Chevalley used these bases to construct analogues of Lie group
s over finite field
s, called Chevalley groups.
The generators of a Lie group are split into the generators H and E such that:

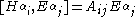
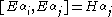
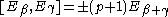
where if is a root and m is the greatest positive integer such that is a root.
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is
a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
constructed by Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
with the property that all structure constants are integers. Chevalley used these bases to construct analogues of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s, called Chevalley groups.
The generators of a Lie group are split into the generators H and E such that:

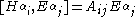
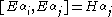
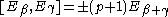
where if is a root and m is the greatest positive integer such that is a root.

