
Chief series
Encyclopedia
In abstract algebra
, a chief series is a maximal normal series
for a group
.
It is similar to a composition series
, though the two concepts are distinct in general: a chief series is a maximal normal series, while a composition series is a maximal subnormal series.
Chief series can be thought of as breaking the group down into simple pieces which may be used to characterize various qualities of the group.
In detail, if G is a group
, then a chief series of G is a finite collection of normal subgroup
s Ni⊆G,
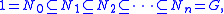
such that each quotient group
Ni+1/Ni, for i = 1, 2,..., n − 1, is a minimal nontrivial normal subgroup of G/Ni. Equivalently, there does not exist any subgroup A normal in G such that Ni < A < Ni+1 for any i. In other words, a chief series may be thought of as "full" in the sense that no normal subgroup of G may be added to it.
The factor groups Ni+1/Ni in a chief series are called the chief factors of the series. Unlike composition factors, chief factors are not necessarily simple
. That is, there may exist a subgroup A normal in Ni+1 with Ni < A < Ni+1 but A is not normal in G. However, the chief factors are always characteristically simple
, that is, they have no non-identity proper characteristic subgroup
s. In particular, a finite chief factor is a direct product of isomorphic simple groups.
and abelian
, and so all of its subgroups are normal and cyclic as well. Supposing there exists a chief series Ni leads to an immediate contradiction: N1 is cyclic and thus is generated by some integer a, however the subgroup generated by 2a is a nontrivial normal subgroup properly contained in N1, contradicting the definition of a chief series.
of the group G, as well as the isomorphism classes
of the chief factors and their multiplicities.
Given any normal subgroup N⊆G, one can always find a chief series in which N is one of the elements (assuming a chief series for G exists in the first place.) Also, if G has a chief series and N is normal in G, then both N and G/N have chief series. The converse also holds: if N is normal in G and both N and G/N have chief series, G has a chief series as well.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a chief series is a maximal normal series
Normal series
In mathematics, a subgroup series is a chain of subgroups:1 = A_0 \leq A_1 \leq \cdots \leq A_n = G.Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups...
for a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
It is similar to a composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
, though the two concepts are distinct in general: a chief series is a maximal normal series, while a composition series is a maximal subnormal series.
Chief series can be thought of as breaking the group down into simple pieces which may be used to characterize various qualities of the group.
Definition
A chief series is a maximal normal series for a group.In detail, if G is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, then a chief series of G is a finite collection of normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s Ni⊆G,
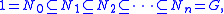
such that each quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
Ni+1/Ni, for i = 1, 2,..., n − 1, is a minimal nontrivial normal subgroup of G/Ni. Equivalently, there does not exist any subgroup A normal in G such that Ni < A < Ni+1 for any i. In other words, a chief series may be thought of as "full" in the sense that no normal subgroup of G may be added to it.
The factor groups Ni+1/Ni in a chief series are called the chief factors of the series. Unlike composition factors, chief factors are not necessarily simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
. That is, there may exist a subgroup A normal in Ni+1 with Ni < A < Ni+1 but A is not normal in G. However, the chief factors are always characteristically simple
Characteristically simple group
In mathematics, in the field of group theory, a group is said to be characteristically simple if it has no proper nontrivial characteristic subgroups. Characteristically simple groups are sometimes also termed elementary groups...
, that is, they have no non-identity proper characteristic subgroup
Characteristic subgroup
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
s. In particular, a finite chief factor is a direct product of isomorphic simple groups.
Existence
Finite groups always have a chief series, though infinite groups need not have a chief series. For example, the group of integers Z with addition as the operation does not have a chief series. To see this, note Z is cyclicCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
and abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, and so all of its subgroups are normal and cyclic as well. Supposing there exists a chief series Ni leads to an immediate contradiction: N1 is cyclic and thus is generated by some integer a, however the subgroup generated by 2a is a nontrivial normal subgroup properly contained in N1, contradicting the definition of a chief series.
Uniqueness
When a chief series for a group exists, it is generally not unique. However, a form of the Jordan–Hölder theorem states that the chief factors of a group are unique up to isomorphism, independent of the particular chief series they are constructed from. In particular, the number of chief factors is an invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of the group G, as well as the isomorphism classes
Isomorphism class
An isomorphism class is a collection of mathematical objects isomorphic to each other.Isomorphism classes are often defined if the exact identity of the elements of the set is considered irrelevant, and the properties of the structure of the mathematical object are studied. Examples of this are...
of the chief factors and their multiplicities.
Other properties
In abelian groups, chief series and composition series are identical, as all subgroups are normal.Given any normal subgroup N⊆G, one can always find a chief series in which N is one of the elements (assuming a chief series for G exists in the first place.) Also, if G has a chief series and N is normal in G, then both N and G/N have chief series. The converse also holds: if N is normal in G and both N and G/N have chief series, G has a chief series as well.

