
Circle map
Encyclopedia


Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a circle map is a member of a family of dynamical systems on the circle first defined by Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
. Kolmogorov proposed this family as a simplified model for driven mechanical rotors (specifically, a free-spinning wheel weakly coupled by a spring to a motor). The circle map equations also describe a simplified model of the phase-locked loop
Phase-locked loop
A phase-locked loop or phase lock loop is a control system that generates an output signal whose phase is related to the phase of an input "reference" signal. It is an electronic circuit consisting of a variable frequency oscillator and a phase detector...
in electronics
Electronics
Electronics is the branch of science, engineering and technology that deals with electrical circuits involving active electrical components such as vacuum tubes, transistors, diodes and integrated circuits, and associated passive interconnection technologies...
. The circle map exhibits certain regions of its parameters where it is locked to the driving frequency (phase-locking or mode-locking in the language of electronic circuits); these are referred to as Arnold tongues, after Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
. Among other applications, the circle map has been used to study the dynamical behaviour of a beating heart
Heart
The heart is a myogenic muscular organ found in all animals with a circulatory system , that is responsible for pumping blood throughout the blood vessels by repeated, rhythmic contractions...
.
Definition
The circle map is given by iterating the map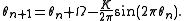
where
 is to be interpreted as polar angle such that its value lies between 0 and 1.
is to be interpreted as polar angle such that its value lies between 0 and 1.It has two parameters, the coupling strength K and the driving phase Ω. As a model for phase-locked loops, Ω may be interpreted as a driving frequency. For K = 0 and Ω irrational, the map reduces to an irrational rotation
Irrational rotation
In mathematical theory of dynamical systems, an irrational rotation is a mapwhere θ is an irrational number. Under the identification of a circle with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation of a circle by a proportion θ of a full...
.
Mode locking
For small to intermediate values of K (that is, in the range of K = 0 to about K = 1), and certain values of Ω, the map exhibits a phenomenon called mode locking or phase locking. In a phase-locked region, the values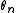 advance essentially as a rational multiple
advance essentially as a rational multipleRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
of n, although they may do so chaotically on the small scale.
The limiting behavior in the mode-locked regions is given by the rotation number
Rotation number
In mathematics, the rotation number is an invariant of homeomorphisms of the circle. It was first defined by Henri Poincaré in 1885, in relation to the precession of the perihelion of a planetary orbit...

which is also sometimes referred to as the map winding number.
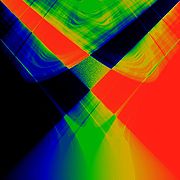
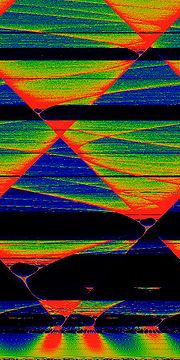
The phase-locked regions, or Arnold tongues, are illustrated in black in the figure above. Each such V-shaped region touches down to a rational value
 in the limit of
in the limit of  . The values of (K,Ω) in one of these regions will all result in a motion such that the rotation number
. The values of (K,Ω) in one of these regions will all result in a motion such that the rotation numberRotation number
In mathematics, the rotation number is an invariant of homeomorphisms of the circle. It was first defined by Henri Poincaré in 1885, in relation to the precession of the perihelion of a planetary orbit...
 . For example, all values of (K,Ω) in the large V-shaped region in the bottom-center of the figure correspond to a rotation number of
. For example, all values of (K,Ω) in the large V-shaped region in the bottom-center of the figure correspond to a rotation number of  . One reason the term "locking" is used is that the individual values
. One reason the term "locking" is used is that the individual values  can be perturbed by rather large random disturbances (up to the width of the tongue, for a given value of K), without disturbing the limiting rotation number. That is, the sequence stays "locked on" to the signal, despite the addition of significant noise to the series
can be perturbed by rather large random disturbances (up to the width of the tongue, for a given value of K), without disturbing the limiting rotation number. That is, the sequence stays "locked on" to the signal, despite the addition of significant noise to the series  . This ability to "lock on" in the presence of noise is central to the utility of phase-locked loop electronic circuit.
. This ability to "lock on" in the presence of noise is central to the utility of phase-locked loop electronic circuit.There is a mode-locked region for every rational number
 . It is sometimes said that the circle map maps the rationals, a set of measure zero at K = 0, to a set of non-zero measure for
. It is sometimes said that the circle map maps the rationals, a set of measure zero at K = 0, to a set of non-zero measure for  . The largest tongues, ordered by size, occur at the Farey fractions. Fixing K and taking a cross-section through this image, so that ω is plotted as a function of Ω gives the Devil's staircase
. The largest tongues, ordered by size, occur at the Farey fractions. Fixing K and taking a cross-section through this image, so that ω is plotted as a function of Ω gives the Devil's staircaseDevil's staircase
In mathematics, a singular function is any function ƒ defined on the interval [a, b] that has the following properties:*ƒ is continuous on [a, b]...
, a shape that is generically similar to the Cantor function
Cantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
.
The circle map also exhibits subharmonic routes
Sarkovskii's theorem
In mathematics, Sharkovskii's theorem, named after Oleksandr Mikolaiovich Sharkovsky, is a result about discrete dynamical systems. One of the implications of the theorem is that if a continuous discrete dynamical system on the real line has a periodic point of period 3, then it must have...
to chaos, that is, period doubling of the form 3,6,12,24,....
Chirikov standard map
The Chirikov standard map is related to the circle map, having similar recurrence relations, which may be written as

with both iterates taken modulo 1. In essence, the standard map introduces a momentum
 which is allowed to dynamically vary, rather than being forced fixed, as it is in the circle map. The standard map is studied in physics
which is allowed to dynamically vary, rather than being forced fixed, as it is in the circle map. The standard map is studied in physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
by means of the kicked rotor Hamiltonian
Hamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
.
External links
- Circle map with interactive Java applet

