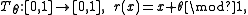Irrational rotation
Encyclopedia
In mathematical theory of dynamical system
s, an irrational rotation is a map
where θ is an irrational number
. Under the identification of a circle
with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation
of a circle
by a proportion θ of a full revolution (i.e. an angle of 2πθ radians). Since θ is irrational, the rotation has infinite order
in the circle group and the map Tθ has no periodic orbits. Moreover, the orbit of any point x under the iterates
of Tθ,

is dense
in the interval [0, 1) or the circle.
s. According to the Denjoy theorem, every orientation-preserving C2-diffeomorphism of the circle with an irrational rotation number
θ is topologically conjugate to Tθ.
An irrational rotation is a measure-preserving ergodic transformation, but it is not mixing
. The Poincaré map
for the dynamical system associated with the Kronecker foliation on a torus
with angle θ is the irrational rotation by θ. C*-algebras associated with irrational rotations, known as irrational rotation algebras, have been extensively studied.
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, an irrational rotation is a map
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
where θ is an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. Under the identification of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
by a proportion θ of a full revolution (i.e. an angle of 2πθ radians). Since θ is irrational, the rotation has infinite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
in the circle group and the map Tθ has no periodic orbits. Moreover, the orbit of any point x under the iterates
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of Tθ,

is dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in the interval [0, 1) or the circle.
Significance
Irrational rotations form a fundamental example in the theory of dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. According to the Denjoy theorem, every orientation-preserving C2-diffeomorphism of the circle with an irrational rotation number
Rotation number
In mathematics, the rotation number is an invariant of homeomorphisms of the circle. It was first defined by Henri Poincaré in 1885, in relation to the precession of the perihelion of a planetary orbit...
θ is topologically conjugate to Tθ.
An irrational rotation is a measure-preserving ergodic transformation, but it is not mixing
Mixing (physics)
In physics, a dynamical system is said to be mixing if the phase space of the system becomes strongly intertwined, according to at least one of several mathematical definitions. For example, a measure-preserving transformation T is said to be strong mixing ifwhenever A and B are any measurable...
. The Poincaré map
Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
for the dynamical system associated with the Kronecker foliation on a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
with angle θ is the irrational rotation by θ. C*-algebras associated with irrational rotations, known as irrational rotation algebras, have been extensively studied.
See also
- Bernoulli map
- Modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
- Toeplitz algebraToeplitz algebraIn operator algebras, the Toeplitz algebra is the C*-algebra generated by the unilateral shift on the Hilbert space l2. Taking l2 to be the Hardy space H2, the Toeplitz algebra consists of elements of the formT_f + K\;...
- Phase locking (Circle Map)