Poincaré map
Encyclopedia
In mathematics
, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré
, is the intersection of a periodic orbit in the state space
of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal
to the flow
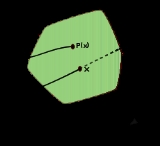
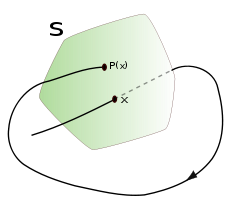
of the system. More precisely, one considers a periodic orbit with initial conditions within a section of the space, which leaves that section afterwards, and observes the point at which this orbit first returns to the section. One then creates a map to send the first point to the second, hence the name first recurrence map. The transversality of the Poincaré section means that periodic orbits starting on the subspace flow through it and not parallel to it.
A Poincaré map can be interpreted as a discrete dynamical system with a state space that is one dimension smaller than the original continuous dynamical system. Because it preserves many properties of periodic and quasiperiodic orbits of the original system and has a lower dimensional state space it is often used for analyzing the original system. In practice this is not always possible as there is no general method to construct a Poincaré map.
A Poincaré map differs from a recurrence plot
in that space, not time, determines when to plot a point. For instance, the locus of the moon when the earth is at perihelion is a recurrence plot; the locus of the moon when it passes through the plane perpendicular to the Earth's orbit and passing through the sun and the earth at perihelion is a Poincaré map. It was used by Michel Hénon
to study the motion of stars in a galaxy
, because the path of a star projected onto a plane looks like a tangled mess, while the Poincaré map shows the structure more clearly.
 Let (R, M, φ) be a global dynamical system, with R the real number
Let (R, M, φ) be a global dynamical system, with R the real number
s, M the phase space
and φ the evolution function. Let γ be a periodic orbit through a point p and S be a local differentiable and transversal section of φ through p, called Poincaré section through p.
Given an open and connected neighborhood U of p, a function

is called Poincaré map for orbit γ on the Poincaré section S through point p if
of a periodic orbit of the original system is closely related to the stability of the fixed point of the corresponding Poincaré map.
Let (R, M, φ) be a differentiable dynamical system with periodic orbit γ through p. Let
be the corresponding Poincaré map through p. We define
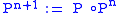
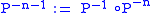
and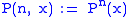
then (Z, U, P) is a discrete dynamical system with state space U and evolution function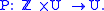
Per definition this system has a fixed point at p.
The periodic orbit γ of the continuous dynamical system is stable
if and only if the fixed point p of the discrete dynamical system is stable.
The periodic orbit γ of the continuous dynamical system is asymptotically stable if and only if the fixed point p of the discrete dynamical system is asymptotically stable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, is the intersection of a periodic orbit in the state space
State space
In the theory of discrete dynamical systems, a state space is a directed graph where each possible state of a dynamical system is represented by a vertex, and there is a directed edge from a to b if and only if ƒ = b where the function f defines the dynamical system.State spaces are...
of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal
Transversality
In mathematics, transversality is a notion that describes how spaces can intersect; transversality can be seen as the "opposite" of tangency, and plays a role in general position. It formalizes the idea of a generic intersection in differential topology...
to the flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
of the system. More precisely, one considers a periodic orbit with initial conditions within a section of the space, which leaves that section afterwards, and observes the point at which this orbit first returns to the section. One then creates a map to send the first point to the second, hence the name first recurrence map. The transversality of the Poincaré section means that periodic orbits starting on the subspace flow through it and not parallel to it.
A Poincaré map can be interpreted as a discrete dynamical system with a state space that is one dimension smaller than the original continuous dynamical system. Because it preserves many properties of periodic and quasiperiodic orbits of the original system and has a lower dimensional state space it is often used for analyzing the original system. In practice this is not always possible as there is no general method to construct a Poincaré map.
A Poincaré map differs from a recurrence plot
Recurrence plot
In descriptive statistics and chaos theory, a recurrence plot is a plot showing, for a given moment in time, the times at which a phase space trajectory visits roughly the same area in the phase space...
in that space, not time, determines when to plot a point. For instance, the locus of the moon when the earth is at perihelion is a recurrence plot; the locus of the moon when it passes through the plane perpendicular to the Earth's orbit and passing through the sun and the earth at perihelion is a Poincaré map. It was used by Michel Hénon
Michel Hénon
Michel Hénon is a mathematician and astronomer. He is currently at the Nice Observatory.In astronomy, Hénon is well known for his contributions to stellar dynamics. In late 1960s and early 1970s he was involved in dynamical evolution of star clusters, in particular the globular clusters...
to study the motion of stars in a galaxy
Galaxy
A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...
, because the path of a star projected onto a plane looks like a tangled mess, while the Poincaré map shows the structure more clearly.
Definition

Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, M the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
and φ the evolution function. Let γ be a periodic orbit through a point p and S be a local differentiable and transversal section of φ through p, called Poincaré section through p.
Given an open and connected neighborhood U of p, a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

is called Poincaré map for orbit γ on the Poincaré section S through point p if
- P(p) = p
- P(U) is a neighborhood of p and P:U → P(U) is a diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
- for every point x in U, the positive semi-orbit of x intersects S for the first time at P(x)
Poincaré maps and stability analysis
Poincaré maps can be interpreted as a discrete dynamical system. The stabilityStability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
of a periodic orbit of the original system is closely related to the stability of the fixed point of the corresponding Poincaré map.
Let (R, M, φ) be a differentiable dynamical system with periodic orbit γ through p. Let

be the corresponding Poincaré map through p. We define

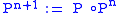
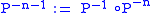
and
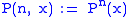
then (Z, U, P) is a discrete dynamical system with state space U and evolution function
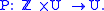
Per definition this system has a fixed point at p.
The periodic orbit γ of the continuous dynamical system is stable
Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
if and only if the fixed point p of the discrete dynamical system is stable.
The periodic orbit γ of the continuous dynamical system is asymptotically stable if and only if the fixed point p of the discrete dynamical system is asymptotically stable.
See also
- Poincaré recurrence
- Stroboscopic map
- Hénon map
- Recurrence plotRecurrence plotIn descriptive statistics and chaos theory, a recurrence plot is a plot showing, for a given moment in time, the times at which a phase space trajectory visits roughly the same area in the phase space...
- Mironenko reflecting functionMironenko reflecting functionThe reflecting function \,F of a dynamical system connects the past state \,x of it with the future state \,x of it by the formula \,x=F...
External Links
- Shivakumar Jolad, Poincare Map and its application to 'Spinning Magnet' problem, (2005)

