Transversality
Encyclopedia
In mathematics
, transversality is a notion that describes how spaces can intersect; transversality can be seen as the "opposite" of tangency
, and plays a role in general position
. It formalizes the idea of a generic intersection in differential topology
. It is defined by considering the linearizations of the intersecting spaces at the points of intersection.
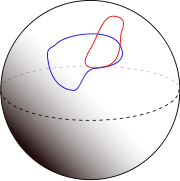Two submanifold
s of a given finite dimensional smooth manifold are said to intersect transversally if at every point of intersection
, their separate tangent spaces at that point together generate the tangent space
of the ambient manifold at that point. Manifolds that do not intersect are vacuously transverse. If the manifolds are of complementary dimension (i.e., their dimensions add up to the dimension of the ambient space
), the condition means that the tangent space to the ambient manifold is the direct sum of the two smaller tangent spaces. If an intersection is transverse, then the intersection will be a submanifold whose codimension
is equal to the sums of the codimensions of the two manifolds. In the absence of the transversality condition the intersection may fail to be a submanifold, having some sort of singular point
.
In particular, this means that transverse submanifolds of complementary dimension intersect in isolated points (i.e., a 0-manifold). If both submanifolds and the ambient manifold are oriented, their intersection is oriented. When the intersection is zero-dimensional, the orientation is simply a plus or minus for each point.
One notation for the transverse intersection of two submanifolds L1 and L2 of a given manifold M is
. This notation can be read in two ways: either as “L1 and L2 intersect transversally” or as an alternative notation for the set-theoretic intersection L1 ∩ L2 of L1 and L2 when that intersection is transverse. In this notation, the definition of transversality reads
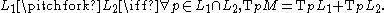
s, this is equivalent to transversality of submanifolds.
Suppose we have transverse maps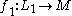 
and 
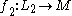where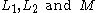 
are manifolds with dimensions 
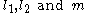respectively.
The meaning of transversality differs a lot depending on the relative dimensions of
and 
. The relationship between transversality and tangency is clearest when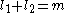 
.
We can consider three separate cases:
class of the manifolds or of their intersections. For example, if manifolds of complementary dimension intersect transversally, the signed sum of the number of their intersection points does not change even if we isotope the manifolds to another transverse intersection. (The intersection points can be counted modulo 2, ignoring the signs, to obtain a coarser invariant.) This descends to a bilinear intersection product on homology classes of any dimension, which is Poincaré dual to the cup product
on cohomology
. Like the cup product, the intersection product is graded-commutative.
. An intersection point between two arcs is transverse if and only if
it is not a tangency, i.e., their tangent lines inside the tangent plane to the surface are distinct.
In a three-dimensional space, transverse curves do not intersect. Curves transverse to surfaces intersect in points, and surfaces transverse to each other intersect in curves. Curves that are tangent to a surface at a point (for instance, curves lying on a surface) do not intersect the surface transversally.
or the related Pontryagin maximum principle, the transversality condition is frequently used to control the types of solutions found in optimization problems. For example, it is a necessary condition for solution curves to problems of the form:
of an oriented manifold's tangent bundle
—i.e. a vector field
—is viewed as a map from the base to the total space, and intersects the zero-section (viewed either as a map or as a submanifold) transversely, then the zero set of the section—i.e. the singularities of the vector field—forms a smooth 0-dimensional submanifold of the base, i.e. a set of signed points. The signs agree with the indices of the vector field, and thus the sum of the signs—i.e. the fundamental class of the zero set—is equal to the Euler characteristic of the manifold. More generally, for a vector bundle
over an oriented smooth closed finite-dimensional manifold, the zero set of a section transverse to the zero section will be a submanifold of the base of codimension equal to the rank of the vector bundle, and its homology class will be Poincaré dual
to the Euler class
of the bundle.
An extremely special case of this is the following: if a differentiable function from reals to the reals has nonzero derivative at a zero of the function, then the zero is simple, i.e. it the graph is transverse to the x-axis at that zero; a zero derivative would mean a horizontal tangent to the curve, which would agree with the tangent space to the x-axis.
For an infinite-dimensional example, the d-bar operator is a section of a certain Banach space
bundle over the space of maps from a Riemann surface
into an almost-complex manifold. The zero set of this section consists of holomorphic maps. If the d-bar operator can be shown to be transverse to the zero-section, this moduli space
will be a smooth manifold. These considerations play a fundamental role in the theory of pseudoholomorphic curves and Gromov–Witten theory. (Note that for this example, the definition of transversality has to be refined in order to deal with Banach spaces!)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, transversality is a notion that describes how spaces can intersect; transversality can be seen as the "opposite" of tangency
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
, and plays a role in general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
. It formalizes the idea of a generic intersection in differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
. It is defined by considering the linearizations of the intersecting spaces at the points of intersection.
Definition
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
s of a given finite dimensional smooth manifold are said to intersect transversally if at every point of intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, their separate tangent spaces at that point together generate the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of the ambient manifold at that point. Manifolds that do not intersect are vacuously transverse. If the manifolds are of complementary dimension (i.e., their dimensions add up to the dimension of the ambient space
Ambient space
An ambient space, ambient configuration space, or electroambient space, is the space surrounding an object.-Mathematics:In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object...
), the condition means that the tangent space to the ambient manifold is the direct sum of the two smaller tangent spaces. If an intersection is transverse, then the intersection will be a submanifold whose codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
is equal to the sums of the codimensions of the two manifolds. In the absence of the transversality condition the intersection may fail to be a submanifold, having some sort of singular point
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
.
In particular, this means that transverse submanifolds of complementary dimension intersect in isolated points (i.e., a 0-manifold). If both submanifolds and the ambient manifold are oriented, their intersection is oriented. When the intersection is zero-dimensional, the orientation is simply a plus or minus for each point.
One notation for the transverse intersection of two submanifolds L1 and L2 of a given manifold M is
. This notation can be read in two ways: either as “L1 and L2 intersect transversally” or as an alternative notation for the set-theoretic intersection L1 ∩ L2 of L1 and L2 when that intersection is transverse. In this notation, the definition of transversality reads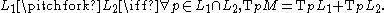Transversality of maps
The notion of transversality of a pair of submanifolds is easily extended to transversality of a submanifold and a map to the ambient manifold, or to a pair of maps to the ambient manifold, by asking whether the pushforwards of the tangent spaces along the preimage of points of intersection of the images generate the entire tangent space of the ambient manifold. If the maps are embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s, this is equivalent to transversality of submanifolds.
Meaning of transversality for different dimensions
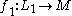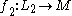and where 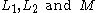are manifolds with dimensions 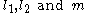respectively.The meaning of transversality differs a lot depending on the relative dimensions of
and . The relationship between transversality and tangency is clearest when 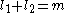.We can consider three separate cases:
- When
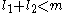, it is impossible for the image of 
and 
's tangent spaces to span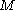 
's tangent space at any point. Thus 
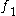and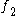 
cannot intersect transversally. - When
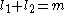, the image of 
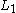and 
's tangent spaces must sum directly to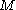 
's tangent space at any point of intersection. Their intersection thus consists of isolated signed points, i.e. a zero-dimensional manifold. - When
this sum needn't be direct. In fact it cannot be direct if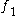 
and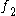 
are immersions at their point of intersection, as happens in the case of embedded submanifolds. If the maps are immersions, the intersection of their images will be a manifold of dimension 
.
Intersection product
Given any two smooth submanifolds, it is possible to perturb either of them by an arbitrarily small amount such that the resulting submanifold intersects transversally with the fixed submanifold. Such perturbations do not affect the homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
class of the manifolds or of their intersections. For example, if manifolds of complementary dimension intersect transversally, the signed sum of the number of their intersection points does not change even if we isotope the manifolds to another transverse intersection. (The intersection points can be counted modulo 2, ignoring the signs, to obtain a coarser invariant.) This descends to a bilinear intersection product on homology classes of any dimension, which is Poincaré dual to the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
on cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
. Like the cup product, the intersection product is graded-commutative.
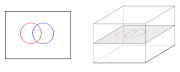
Examples of transverse intersections
The simplest non-trivial example of transversality is of arcs in a surfaceSurface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
. An intersection point between two arcs is transverse if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is not a tangency, i.e., their tangent lines inside the tangent plane to the surface are distinct.
In a three-dimensional space, transverse curves do not intersect. Curves transverse to surfaces intersect in points, and surfaces transverse to each other intersect in curves. Curves that are tangent to a surface at a point (for instance, curves lying on a surface) do not intersect the surface transversally.
Optimal control
In fields utilizing the calculus of variationsCalculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
or the related Pontryagin maximum principle, the transversality condition is frequently used to control the types of solutions found in optimization problems. For example, it is a necessary condition for solution curves to problems of the form:
- Minimize
where one or both of the endpoints of the curve are not fixed. In many of these problems, the solution satisfies the condition that the solution curve should cross transversally the nullclineNullclineNullclines, sometimes called zero-growth isoclines, are encountered in a system of ordinary differential equationsx_1'=f_1x_2'=f_2In a two-dimensional linear system, the nullclines can be represented by two lines on a two-dimensional plot.-External links:* from MIT OpenCourseWare*...
or some other curve describing terminal conditions.
Smoothness of solution spaces
Using Sard's theorem, whose hypothesis is a special case of the transversality of maps, it can be shown that transverse intersections between submanifolds of a space of complementary dimensions or between submanifolds and maps to a space are themselves smooth submanifolds. For instance, if a smooth sectionSection (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of an oriented manifold's tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
—i.e. a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
—is viewed as a map from the base to the total space, and intersects the zero-section (viewed either as a map or as a submanifold) transversely, then the zero set of the section—i.e. the singularities of the vector field—forms a smooth 0-dimensional submanifold of the base, i.e. a set of signed points. The signs agree with the indices of the vector field, and thus the sum of the signs—i.e. the fundamental class of the zero set—is equal to the Euler characteristic of the manifold. More generally, for a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over an oriented smooth closed finite-dimensional manifold, the zero set of a section transverse to the zero section will be a submanifold of the base of codimension equal to the rank of the vector bundle, and its homology class will be Poincaré dual
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
to the Euler class
Euler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
of the bundle.
An extremely special case of this is the following: if a differentiable function from reals to the reals has nonzero derivative at a zero of the function, then the zero is simple, i.e. it the graph is transverse to the x-axis at that zero; a zero derivative would mean a horizontal tangent to the curve, which would agree with the tangent space to the x-axis.
For an infinite-dimensional example, the d-bar operator is a section of a certain Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
bundle over the space of maps from a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
into an almost-complex manifold. The zero set of this section consists of holomorphic maps. If the d-bar operator can be shown to be transverse to the zero-section, this moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
will be a smooth manifold. These considerations play a fundamental role in the theory of pseudoholomorphic curves and Gromov–Witten theory. (Note that for this example, the definition of transversality has to be refined in order to deal with Banach spaces!)