
Mironenko reflecting function
Encyclopedia
The reflecting function  of a dynamical system
of a dynamical system
connects the past state of it with the future state
of it with the future state 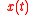 of it by the formula
of it by the formula 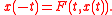 The concept of the reflecting function was introduсed by Vladimir Ivanovich Mironenko.
The concept of the reflecting function was introduсed by Vladimir Ivanovich Mironenko.
 with the general solution
with the general solution  in Cauchy form Reflecting Function is defined by formula
in Cauchy form Reflecting Function is defined by formula 
 is periodic in
is periodic in  with respect to
with respect to  , then
, then  is a transformation (Poincaré map
is a transformation (Poincaré map
) periodic in of the differential system
of the differential system  Therefore the knowledge of the Reflecting Function give us the opportunity to find out the initial date
Therefore the knowledge of the Reflecting Function give us the opportunity to find out the initial date 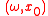 of periodic solutions of the differential system and investigate the stability
of periodic solutions of the differential system and investigate the stability
of those solutions.
For the Reflecting Function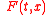 of the system
of the system  the basic relation
the basic relation
is holding.
Therefore we have an opportunity sometimes to find Poincaré map of the non-integrable in quadrature
systems even in elementary functions.
 of a dynamical system
of a dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
connects the past state
 of it with the future state
of it with the future state 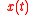 of it by the formula
of it by the formula 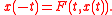 The concept of the reflecting function was introduсed by Vladimir Ivanovich Mironenko.
The concept of the reflecting function was introduсed by Vladimir Ivanovich Mironenko.Definition
For the differential system with the general solution
with the general solution  in Cauchy form Reflecting Function is defined by formula
in Cauchy form Reflecting Function is defined by formula 
Application
If a vector-function is periodic in
is periodic in  with respect to
with respect to  , then
, then  is a transformation (Poincaré map
is a transformation (Poincaré mapPoincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
) periodic in
 of the differential system
of the differential system  Therefore the knowledge of the Reflecting Function give us the opportunity to find out the initial date
Therefore the knowledge of the Reflecting Function give us the opportunity to find out the initial date 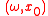 of periodic solutions of the differential system and investigate the stability
of periodic solutions of the differential system and investigate the stabilityLyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
of those solutions.
For the Reflecting Function
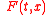 of the system
of the system  the basic relation
the basic relationis holding.
Therefore we have an opportunity sometimes to find Poincaré map of the non-integrable in quadrature
Quadrature
Quadrature may refer to:In signal processing:*Quadrature amplitude modulation , a modulation method of using both an carrier wave and a 'quadrature' carrier wave that is 90° out of phase with the main, or in-phase, carrier...
systems even in elementary functions.
Literature
- Мироненко В. И. Отражающая функция и периодические решения дифференциальных уравнений. — Минск, Университетское, 1986. — 76 с.
- Мироненко В. И. Отражающая функция и исследование многомерных дифференциальных систем. — Гомель: Мин. образов. РБ, ГГУ им. Ф. Скорины, 2004. — 196 с.


